


Next: Noise with Power-law trends
Up: Noise with sinusoidal trend
Previous: DFA-1 on noise with
Higher order DFA on pure sinusoidal trend
In the previous Sec. 4.2, we discussed how sinusoidal
trends affect the scaling behavior of correlated noise when the
DFA-1 method is applied. Since DFA-1 removes only constant trends in
data, it is natural to ask how the observed scaling results will
change when we apply DFA of order  designed to remove
polynomial trends of order lower than
designed to remove
polynomial trends of order lower than  . In this section, we
first consider the rms fluctuation
. In this section, we
first consider the rms fluctuation 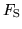 for a sinusoidal
signal and then we study the scaling and crossover properties of
for a sinusoidal
signal and then we study the scaling and crossover properties of
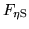 for correlated noise with superimposed sinusoidal
signal when higher order DFA is used.
for correlated noise with superimposed sinusoidal
signal when higher order DFA is used.
We find that the rms fluctuation function 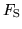 does not
depend on the length of the signal
does not
depend on the length of the signal  , and preserves a
similar shape when different order-
, and preserves a
similar shape when different order- DFA method is used
[Fig. 9]. In particular,
DFA method is used
[Fig. 9]. In particular, 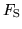 exhibits a crossover
at a scale
exhibits a crossover
at a scale 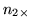 proportional to the period
proportional to the period 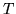 of the
sinusoidal:
of the
sinusoidal:
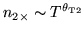 with
with
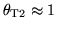 . The crossover scale shifts to larger values for
higher order
. The crossover scale shifts to larger values for
higher order  [Fig. 5 and
Fig. 9]. For the scale
[Fig. 5 and
Fig. 9]. For the scale 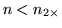 ,
, 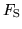 exhibits an apparent scaling:
exhibits an apparent scaling:
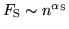 with an effective exponent
with an effective exponent
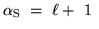 . For DFA-1, we
have
. For DFA-1, we
have 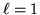 and recover
and recover
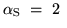 as shown in
Eq. (12). For
as shown in
Eq. (12). For 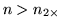 ,
, 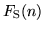 is a
constant independent of the scale
is a
constant independent of the scale  , and of the order
, and of the order
 of the DFA method in agreement with Eq. (13).
of the DFA method in agreement with Eq. (13).
Next, we consider
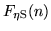 when DFA-
when DFA- with a higher order
with a higher order  is used. We find that for all orders
is used. We find that for all orders  ,
,
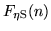 does not depend on the length of the
signal
does not depend on the length of the
signal  and exhibits three crossovers -- at small,
intermediate and large scales -- similar behavior is reported for
DFA-1 in Fig. 6. Since the crossover at small
scales,
and exhibits three crossovers -- at small,
intermediate and large scales -- similar behavior is reported for
DFA-1 in Fig. 6. Since the crossover at small
scales, 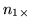 , and the crossover at large scale,
, and the crossover at large scale,
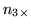 , result from the ``competition'' between the
scaling of the correlated noise and the effect of the sinusoidal
trend (Figs. 6 and 7), using
the superposition rule [Eq. (10)] we can estimate
, result from the ``competition'' between the
scaling of the correlated noise and the effect of the sinusoidal
trend (Figs. 6 and 7), using
the superposition rule [Eq. (10)] we can estimate
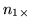 and
and 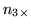 as the intercepts of
as the intercepts of
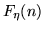 and
and 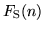 for the general case of DFA-
for the general case of DFA- .
.
For 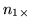 we find the following dependence on the period
we find the following dependence on the period
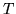 , amplitude
, amplitude 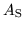 , the correlation exponent
, the correlation exponent 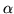 of
the noise, and the order
of
the noise, and the order  of the DFA-
of the DFA- method:
method:
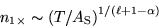 |
(16) |
For DFA-1, we have 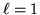 and we recover Eq. (14). In
addition,
and we recover Eq. (14). In
addition, 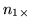 is shifted to larger scales when higher
order DFA-
is shifted to larger scales when higher
order DFA- is applied, due to the fact that the value of
is applied, due to the fact that the value of
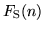 decreases when
decreases when  increases (
increases (
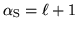 , see Fig. 9).
, see Fig. 9).
For the third crossover observed in
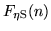 at large
scale
at large
scale 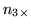 we find for all orders
we find for all orders  of the
DFA-
of the
DFA- the following scaling relation:
the following scaling relation:
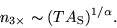 |
(17) |
Since the scaling function
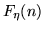 for correlated noise
shifts vertically to lower values when higher order DFA-
for correlated noise
shifts vertically to lower values when higher order DFA- is used [see the discussion in Appendix 7.1 and
Sec. 5.2],
is used [see the discussion in Appendix 7.1 and
Sec. 5.2], 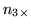 exhibits a slight shift to
larger scales.
exhibits a slight shift to
larger scales.
For the crossover 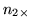 in
in
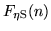 at
at
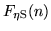 at intermediate scales, we find:
at intermediate scales, we find:
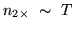 .
This relation is independent of the order
.
This relation is independent of the order  of the DFA and is
identical to the relation found for
of the DFA and is
identical to the relation found for 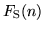 [Eq. (11)].
[Eq. (11)]. 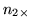 also exhibits a shift to larger
scales when higher order DFA is used [see Fig. 9].
also exhibits a shift to larger
scales when higher order DFA is used [see Fig. 9].
The reported here features of the crossovers in
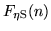 can be used to identify low-frequency sinusoidal trends in
noisy data, and to recognize their effects on the scaling
properties of the data. This information may be useful when
quantifying correlation properties in data by means of scaling
analysis.
can be used to identify low-frequency sinusoidal trends in
noisy data, and to recognize their effects on the scaling
properties of the data. This information may be useful when
quantifying correlation properties in data by means of scaling
analysis.
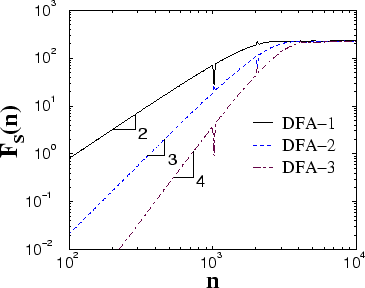
Figure 9:
Comparison of the results of different
order DFA on a sinusoidal trend. The sinusoidal trend is
given by the function
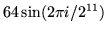 and the
length of the signal is
and the
length of the signal is
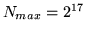 . The spurious singularities
(spikes) arise from the discrete data we use for the sinusoidal function.
. The spurious singularities
(spikes) arise from the discrete data we use for the sinusoidal function.
 |



Next: Noise with Power-law trends
Up: Noise with sinusoidal trend
Previous: DFA-1 on noise with
Zhi Chen
2002-08-28
