


Next: DFA-1 on sinusoidal trend
Up: Effect of Trends on
Previous: DFA-2 on noise with
Noise with sinusoidal trend
In this section, we study the effect of sinusoidal trends on the
scaling properties of noisy signals. For a signal which is a
superposition of correlated noise and sinusoidal trend, we find
that based on the superposition rule (Appendix 7.2) the
DFA rms fluctuation function can be expressed as
![\begin{displaymath}
\left[F_{\rm\eta S}(n)\right]^2 = \left[F_{\rm\eta}(n)\right]^2 + \left[F_{\rm S}(n)\right]^2,
\end{displaymath}](img209.png) |
(10) |
where
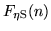 is the rms fluctuation
function of noise with a sinusoidal trend, and
is the rms fluctuation
function of noise with a sinusoidal trend, and 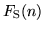 is
for the sinusoidal trend. First we consider the application of DFA-1 to a sinusoidal trend. Next we study the scaling behavior and the features of crossovers in
is
for the sinusoidal trend. First we consider the application of DFA-1 to a sinusoidal trend. Next we study the scaling behavior and the features of crossovers in
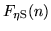 for the superposition of correlated noise and sinusoidal trend
employing the superposition rule [Eq.(10)]. At the end
of this section, we discuss the results obtained from higher order DFA.
for the superposition of correlated noise and sinusoidal trend
employing the superposition rule [Eq.(10)]. At the end
of this section, we discuss the results obtained from higher order DFA.
Subsections
Zhi Chen
2002-08-28