Table II: The crossover exponents
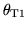 and and
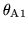 characterizing the power-law dependence of
characterizing the power-law dependence of 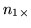 on the
period on the
period 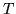 and amplitude and amplitude 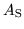 obtained from simulations: obtained from simulations:
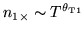 and and
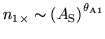 for different value of the
correlation exponent for different value of the
correlation exponent 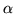 of noise
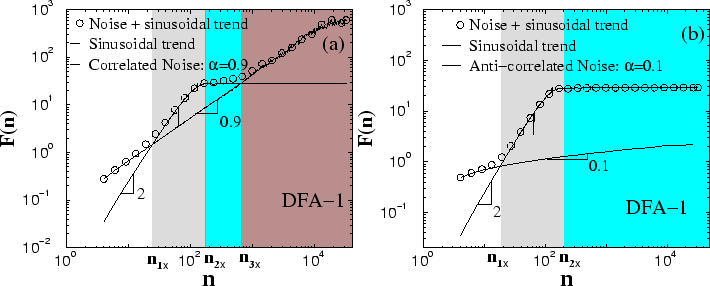
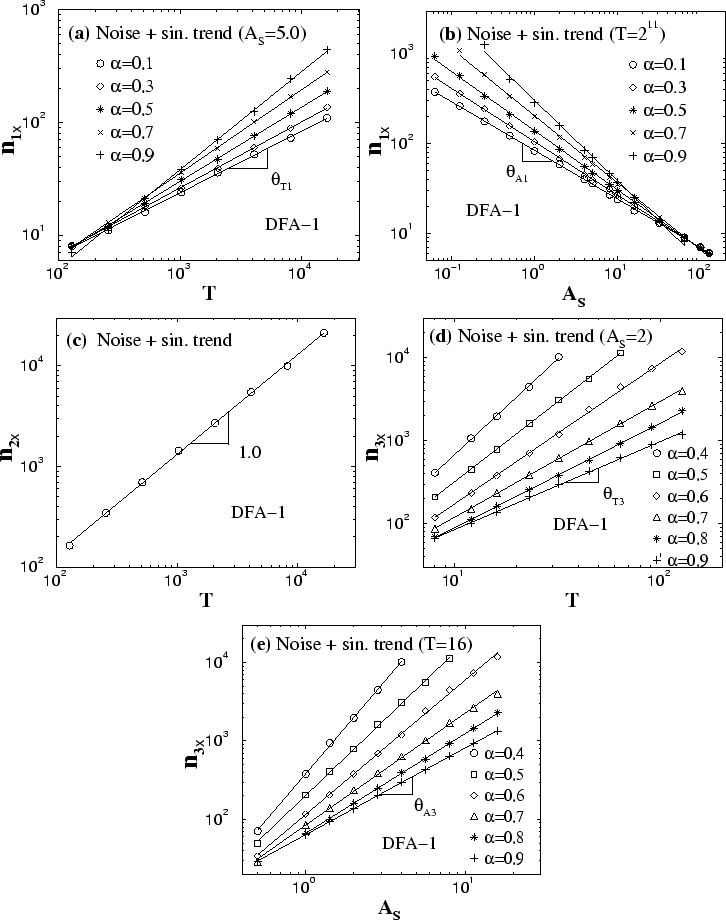
[Fig. 8(a)(b)]. The values of of noise
[Fig. 8(a)(b)]. The values of
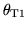 and and
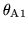 are in good agreement with the analytical predictions are in good agreement with the analytical predictions
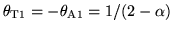 [Eq. (14)].
[Eq. (14)].
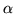 |
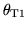 |
-
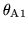 |
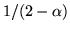 |
| 0.1 |
0.55 |
0.54 |
0.53 |
| 0.3 |
0.58 |
0.59 |
0.59 |
| 0.5 |
0.66 |
0.66 |
0.67 |
| 0.7 |
0.74 |
0.75 |
0.77 |
| 0.9 |
0.87 |
0.90 |
0.91 |
|