


Next: DFA-1 on noise with
Up: Noise with sinusoidal trend
Previous: Noise with sinusoidal trend
DFA-1 on sinusoidal trend
Given a sinusoidal trend
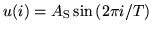 (
(
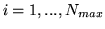 ), where
), where 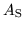 is the amplitude of the
signal and
is the amplitude of the
signal and 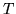 is the period, we find that the rms fluctuation
function
is the period, we find that the rms fluctuation
function 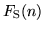 does not depend on the length of the
signal
does not depend on the length of the
signal  , and has the same shape for different amplitudes
and different periods [Fig. 5]. We find a
crossover at scale corresponding to the period of the sinusoidal
trend
, and has the same shape for different amplitudes
and different periods [Fig. 5]. We find a
crossover at scale corresponding to the period of the sinusoidal
trend
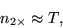 |
(11) |
and does not depend on the amplitude 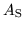 . We
call this crossover
. We
call this crossover 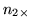 for convenience, as we will see later. For
for convenience, as we will see later. For
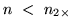 , the rms fluctuation
, the rms fluctuation 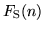 exhibits an
apparent scaling with the same exponent as
exhibits an
apparent scaling with the same exponent as 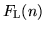 for the
linear trend [see Eq. (7)]:
for the
linear trend [see Eq. (7)]:
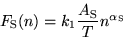 |
(12) |
where 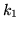 is a constant independent of the length
is a constant independent of the length  , of
the period
, of
the period 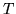 and the amplitude
and the amplitude 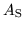 of the sinusoidal
signal, and of the box size
of the sinusoidal
signal, and of the box size  . As for the linear trend
[Eq.(7)], we obtain
. As for the linear trend
[Eq.(7)], we obtain
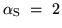 because
at small scales (box size
because
at small scales (box size  ) the sinusoidal function is
dominated by a linear term. For
) the sinusoidal function is
dominated by a linear term. For
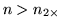 , due to the
periodic property of the sinusoidal trend,
, due to the
periodic property of the sinusoidal trend, 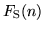 is a
constant independent of the scale
is a
constant independent of the scale  :
:
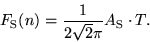 |
(13) |
The period 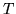 and the amplitude
and the amplitude 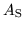 also affects the
vertical shift of
also affects the
vertical shift of 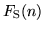 in both regions. We note that in
Eqs.(12) and (13),
in both regions. We note that in
Eqs.(12) and (13), 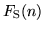 is proportional to the
amplitude
is proportional to the
amplitude 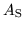 , a behavior which is also observed for the
linear trend [Eq. (7)].
, a behavior which is also observed for the
linear trend [Eq. (7)].
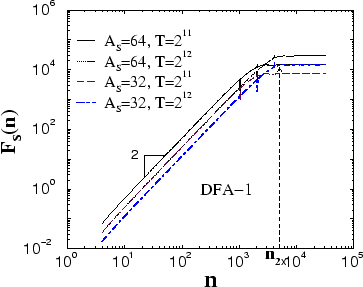
Figure 5:
Root mean square fluctuation function 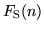 for
sinusoidal functions of length
for
sinusoidal functions of length
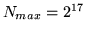 with different
amplitude
with different
amplitude 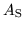 and period
and period 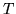 . All curves exhibit a
crossover at
. All curves exhibit a
crossover at
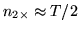 , with a slope
, with a slope
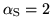 for
for
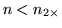 , and a flat region for
, and a flat region for
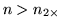 . There are some spurious singularities at
. There are some spurious singularities at
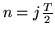 (
(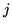 is a positive integer) shown by the spikes.
is a positive integer) shown by the spikes.
 |



Next: DFA-1 on noise with
Up: Noise with sinusoidal trend
Previous: Noise with sinusoidal trend
Zhi Chen
2002-08-28
