


Next: Dependence of on the
Up: Noise with Power-law trends
Previous: Dependence of on the
Dependence of  on the order
on the order  of DFA
of DFA
Another factor that affects the rms fluctuation function of the power-law trend  , is the order
, is the order  of the DFA method used. We first take into account that:
of the DFA method used. We first take into account that:
- (1) for integer values of the power
 , the power-law trend
, the power-law trend
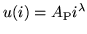 is a polynomial trend which can be perfectly filtered out by the DFA method of order
is a polynomial trend which can be perfectly filtered out by the DFA method of order 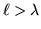 , and as discussed in Sec. 3.2 and Sec. 5.1 [see Fig. 11(b) and (c)], there is no scaling for
, and as discussed in Sec. 3.2 and Sec. 5.1 [see Fig. 11(b) and (c)], there is no scaling for  . Therefore, in this section we consider only non-integer values of
. Therefore, in this section we consider only non-integer values of  .
.
- (2) for a given value of the power
 , the effective exponent
, the effective exponent
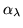 can take different values depending on the order
can take different values depending on the order  of the DFA method we use [see Fig. 11] -- e.g. for fixed
of the DFA method we use [see Fig. 11] -- e.g. for fixed
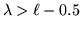 ,
,
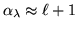 . Therefore, in this section, we consider only the case when
. Therefore, in this section, we consider only the case when
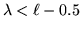 (Region II and III).
(Region II and III).
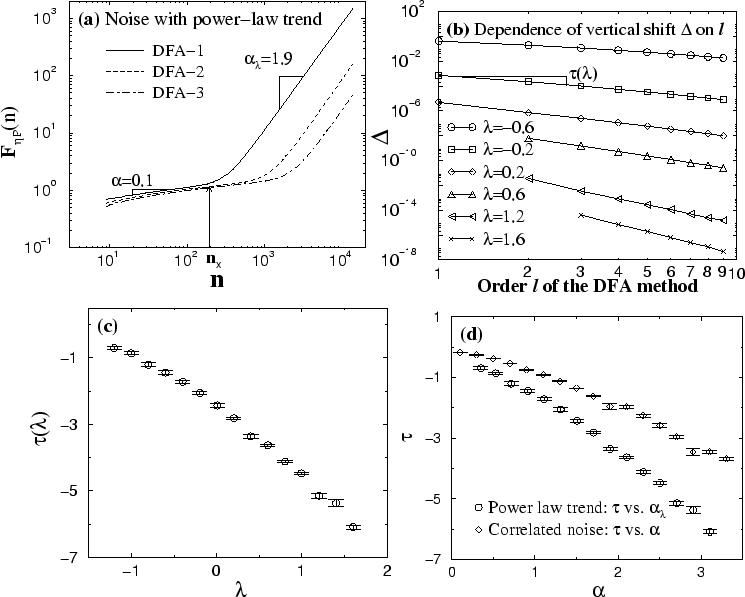
Figure 12:
Effect of higher order DFA- on the rms fluctuation function
on the rms fluctuation function
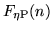 for correlated noise with superimposed power-law trend. (a)
for correlated noise with superimposed power-law trend. (a)
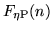 for anticorrelated noise with correlation exponent
for anticorrelated noise with correlation exponent 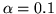 and a power-law
and a power-law
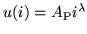 , where
, where
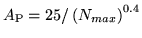 ,
,
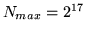 and
and  . Results for different order
. Results for different order 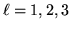 of the DFA method show (i) a clear crossover from a region at small scales where the noise dominates
of the DFA method show (i) a clear crossover from a region at small scales where the noise dominates
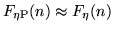 , to a region at larger scales where the power-law trend dominates
, to a region at larger scales where the power-law trend dominates
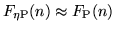 , and (ii) a vertical shift
, and (ii) a vertical shift  in
in
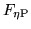 with increasing
with increasing  . (b) Dependence of the vertical shift
. (b) Dependence of the vertical shift 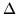 in the rms fluctuation function
in the rms fluctuation function 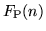 for power-law trend on the order
for power-law trend on the order  of DFA-
of DFA- for different values of
for different values of  :
:
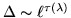 . We define the vertical shift
. We define the vertical shift 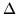 as the y-intercept of
as the y-intercept of 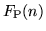 :
:
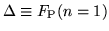 . Note, that we consider only non-integer values for
. Note, that we consider only non-integer values for  and that we consider the region
and that we consider the region
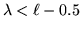 . Thus, for all values of
. Thus, for all values of  the minimal order
the minimal order  that can be used in the DFA method is
that can be used in the DFA method is
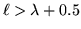 . e.g. for
. e.g. for 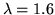 the minimal order of the DFA that can be used is
the minimal order of the DFA that can be used is 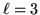 (for details see Fig. 11(b)).
(c) Dependence of
(for details see Fig. 11(b)).
(c) Dependence of 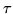 on the power
on the power  (error bars indicate the regression error for the fits of
(error bars indicate the regression error for the fits of 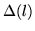 in (b)).
(d) Comparison of
in (b)).
(d) Comparison of
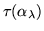 for
for 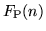 and
and 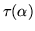 for
for
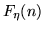 . Faster decay of
. Faster decay of
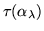 indicates larger vertical shifts for
indicates larger vertical shifts for 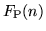 compared to
compared to
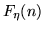 with increasing order
with increasing order  of the DFA-
of the DFA- .
.
 |
Since higher order DFA- provides a better fit for the data, the fluctuation function
provides a better fit for the data, the fluctuation function 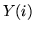 (Eq. (3)) decreases with increasing order
(Eq. (3)) decreases with increasing order  . This leads to a vertical shift to smaller values of the rms fluctuation function
. This leads to a vertical shift to smaller values of the rms fluctuation function 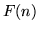 (Eq. (4)). Such a vertical shift is observed for the rms fluctuation function
(Eq. (4)). Such a vertical shift is observed for the rms fluctuation function
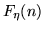 for correlated noise (see Appendix 7.1), as well as for the rms fluctuation function of power-law trend
for correlated noise (see Appendix 7.1), as well as for the rms fluctuation function of power-law trend  . Here we ask how this vertical shift in
. Here we ask how this vertical shift in
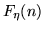 and
and  depends on the order
depends on the order  of the DFA method, and if this shift has different properties for
of the DFA method, and if this shift has different properties for
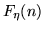 compared to
compared to  . This information can help identify power-law trends in noisy data, and can be used to differentiate crossovers separating scaling regions with different types of correlations, and crossovers which are due to effects of power-law trends.
. This information can help identify power-law trends in noisy data, and can be used to differentiate crossovers separating scaling regions with different types of correlations, and crossovers which are due to effects of power-law trends.
We consider correlated noise with a superposed power-law trend,
where the crossover in
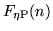 at large scales
at large scales  results from the dominant effect of the power-law trend --
results from the dominant effect of the power-law trend --
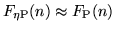 (Eq. (18) and
Fig. 10(a)). We choose the power
(Eq. (18) and
Fig. 10(a)). We choose the power 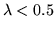 , a
range where for all orders
, a
range where for all orders  of the DFA method the effective
exponent
of the DFA method the effective
exponent
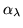 of
of  remains the same --
i.e.
remains the same --
i.e.
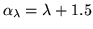 (region II in
Fig. 11(b)). For a superposition of an anticorrelated
noise and power-law trend with
(region II in
Fig. 11(b)). For a superposition of an anticorrelated
noise and power-law trend with  , we observe
a crossover in the scaling behavior of
, we observe
a crossover in the scaling behavior of
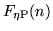 , from a
scaling region characterized by the correlation exponent
, from a
scaling region characterized by the correlation exponent
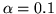 of the noise, where
of the noise, where
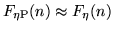 , to a region characterized by an effective exponent
, to a region characterized by an effective exponent
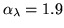 , where
, where
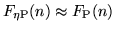 , for all orders
, for all orders 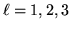 of the DFA-
of the DFA- method
[Fig. 12(a)]. We also find that the crossover
of
method
[Fig. 12(a)]. We also find that the crossover
of
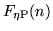 shifts to larger scales when the order
shifts to larger scales when the order
 of DFA-
of DFA- increases, and that there is a vertical shift
of
increases, and that there is a vertical shift
of
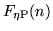 to lower values. This vertical shift in
to lower values. This vertical shift in
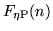 at large scales, where
at large scales, where
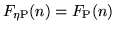 , appears to be different in
magnitude when different order
, appears to be different in
magnitude when different order  of the DFA-
of the DFA- method is
used [Fig. 12(a)]. We also
observe a less pronounced vertical shift at small scales where
method is
used [Fig. 12(a)]. We also
observe a less pronounced vertical shift at small scales where
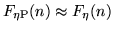 .
.
Next, we ask how these vertical shifts depend on
the order  of DFA-
of DFA- . We define the vertical shift
. We define the vertical shift 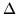 as the y-intercept of
as the y-intercept of  :
:
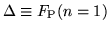 . We find that the vertical shift
. We find that the vertical shift 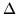 in
in  for power-law trend follows a power law:
for power-law trend follows a power law:
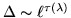 . We tested this relation
for orders up to
. We tested this relation
for orders up to 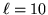 , and we find that it holds for
different values of the power
, and we find that it holds for
different values of the power  of the power-law trend
[Fig. 12(b)]. Using Eq. (19) we can write:
of the power-law trend
[Fig. 12(b)]. Using Eq. (19) we can write:
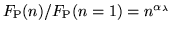 , i.e.
, i.e.
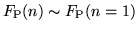 . Since
. Since
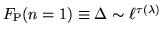 [Fig. 12(b)], we find that:
[Fig. 12(b)], we find that:
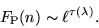 |
(20) |
We also find that the exponent
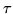 is negative and is a decreasing function of the power
is negative and is a decreasing function of the power
 [Fig. 12(c)]. Because the effective
exponent
[Fig. 12(c)]. Because the effective
exponent
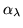 which characterizes
which characterizes  depends on the power
depends on the power  [see Fig. 11(b)], we
can express the exponent
[see Fig. 11(b)], we
can express the exponent 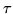 as a function of
as a function of
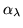 as we show in Fig. 12(d).
This representation can help us compare the behavior of the
vertical shift
as we show in Fig. 12(d).
This representation can help us compare the behavior of the
vertical shift 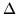 in
in  with the shift in
with the shift in
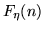 . For correlated noise with different correlation
exponent
. For correlated noise with different correlation
exponent 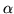 , we observe a similar power-law relation
between the vertical shift in
, we observe a similar power-law relation
between the vertical shift in
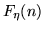 and the order
and the order
 of DFA-
of DFA- :
:
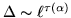 , where
, where
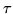 is also a negative exponent which decreases with
is also a negative exponent which decreases with 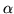 .
In Fig. 12(d) we compare
.
In Fig. 12(d) we compare
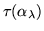 for
for  with
with 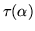 for
for
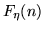 , and find that for any
, and find that for any
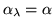 ,
,
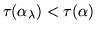 . This difference between the vertical shift for
correlated noise and for a power-law trend can be utilized to
recognize effects of power-law trends on the scaling properties of
data.
. This difference between the vertical shift for
correlated noise and for a power-law trend can be utilized to
recognize effects of power-law trends on the scaling properties of
data.



Next: Dependence of on the
Up: Noise with Power-law trends
Previous: Dependence of on the
Zhi Chen
2002-08-28
