


Next: Conclusion and Summary
Up: Noise with Power-law trends
Previous: Dependence of on the
We have seen that, taking into account the effects of the power  (Eq. (19)), the order
(Eq. (19)), the order  of DFA-
of DFA- (Eq. (20)) and the effect of the length of the signal
(Eq. (20)) and the effect of the length of the signal  (Eq. (21)), we reach the following expression for the rms fluctuation function
(Eq. (21)), we reach the following expression for the rms fluctuation function  for a power-law trend
for a power-law trend
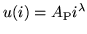 :
:
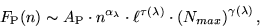 |
(22) |
For correlated noise, the rms fluctuation function
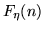 depends on the box size
depends on the box size  (Eq. (6)) and on the order
(Eq. (6)) and on the order  of DFA-
of DFA- (Sec. 5.2 and Fig. 12(a), (d)), and does not depend on the length of the signal
(Sec. 5.2 and Fig. 12(a), (d)), and does not depend on the length of the signal  . Thus we have the following expression for
. Thus we have the following expression for
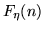
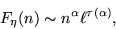 |
(23) |
To estimate the crossover scale 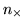 observed in the apparent scaling of
observed in the apparent scaling of
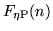 for a correlated noise superposed with a power-law trend [Fig. 10(a), (b) and Fig. 12(a)], we employ the superposition rule (Eq. (18)). From Eq. (22) and Eq. (23), we obtain
for a correlated noise superposed with a power-law trend [Fig. 10(a), (b) and Fig. 12(a)], we employ the superposition rule (Eq. (18)). From Eq. (22) and Eq. (23), we obtain 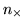 as the intercept between
as the intercept between  and
and
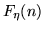 :
:
![\begin{displaymath}
n_{\times} \sim \left[A l^{\tau(\lambda)-\tau(\alpha)} \lef...
...max}\right )^{\gamma}\right]^{1/(\alpha-\alpha_{\lambda})}.
\end{displaymath}](img338.png) |
(24) |
To test the validity of this result, we consider the case of correlated noise with a linear trend. For the case of a linear trend (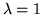 ) when DFA-1 (
) when DFA-1 (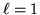 ) is applied, we have
) is applied, we have
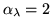 (see Appendix 7.3 and Sec. 5.1, Fig. 11(b)). Since in this case
(see Appendix 7.3 and Sec. 5.1, Fig. 11(b)). Since in this case
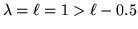 we have
we have
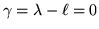 (see Sec.5.3 Fig. 13(b)), and from Eq. (24) we recover Eq. (9).
(see Sec.5.3 Fig. 13(b)), and from Eq. (24) we recover Eq. (9).



Next: Conclusion and Summary
Up: Noise with Power-law trends
Previous: Dependence of on the
Zhi Chen
2002-08-28