


Next: Dependence of on the
Up: Noise with Power-law trends
Previous: Noise with Power-law trends
Dependence of  on the power
on the power 
First we study how the rms fluctuation function  for a
power-law trend
for a
power-law trend
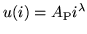 depends on the power
depends on the power  . We find that
. We find that
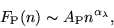 |
(19) |
where
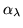 is the effective exponent for the power-law trend. For positive
is the effective exponent for the power-law trend. For positive  we observe no crossovers in
we observe no crossovers in  (Fig. 10(a)). However, for negative
(Fig. 10(a)). However, for negative  there is a crossover in
there is a crossover in  at small scales
at small scales  (Fig. 10(b)), and we find that this crossover becomes even more pronounced with decreasing
(Fig. 10(b)), and we find that this crossover becomes even more pronounced with decreasing  or increasing the order
or increasing the order  of the DFA method, and is also shifted to larger scales [Fig. 11(a)].
of the DFA method, and is also shifted to larger scales [Fig. 11(a)].
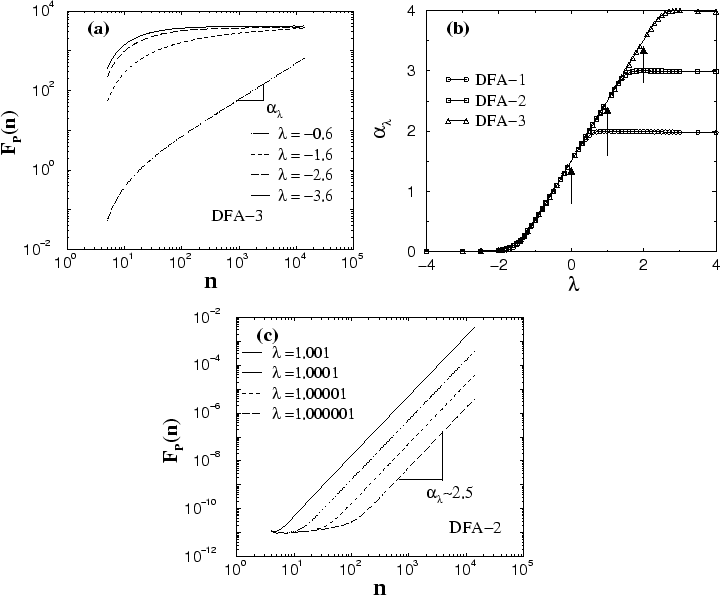
Figure 11:
Scaling behavior of rms fluctuation function 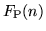 for power-law trends,
for power-law trends,
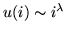 , where
, where
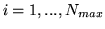 and
and
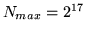 is the length of the signal. (a) For
is the length of the signal. (a) For 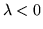 ,
, 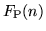 exhibits crossover at small scales which is more pronounced with increasing the order
exhibits crossover at small scales which is more pronounced with increasing the order  of DFA-
of DFA- and decreasing the value of
and decreasing the value of  . Such crossover is not observed for
. Such crossover is not observed for 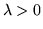 when
when
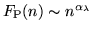 for all scales
for all scales  [see Fig. 10(a)]. (b) Dependence of the effective exponent
[see Fig. 10(a)]. (b) Dependence of the effective exponent
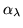 on the power
on the power  for different order
for different order 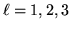 of the DFA method. Three regions are observed depending on the order
of the DFA method. Three regions are observed depending on the order  of the DFA: region I (
of the DFA: region I (
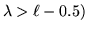 , where
, where
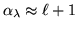 ; region II (
; region II (
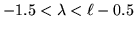 ), where
), where
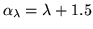 ; region III (
; region III (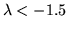 ), where
), where
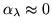 . We note that for integer values of the power
. We note that for integer values of the power
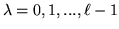 , where
, where  is the order of DFA we used, there is no scaling for
is the order of DFA we used, there is no scaling for 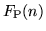 and
and
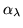 is not defined, as indicated by the arrows. (c) Asymptotic behavior near integer values of
is not defined, as indicated by the arrows. (c) Asymptotic behavior near integer values of  .
. 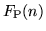 is plotted for
is plotted for
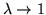 when DFA-2 is used. Even for
when DFA-2 is used. Even for
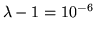 , we observe at large scales
, we observe at large scales  a region with an effective exponent
a region with an effective exponent
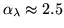 , This region is shifted to infinitely large scales when
, This region is shifted to infinitely large scales when 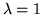 .
.
 |
Next, we study how the effective exponent
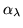 for
for  depends on the value of the power
depends on the value of the power  for the power-law trend. We examine the scaling of
for the power-law trend. We examine the scaling of  and estimate
and estimate
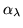 for
for 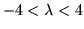 . In the cases when
. In the cases when  exhibits a crossover, in order to obtain
exhibits a crossover, in order to obtain
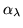 we fit the range of larger scales to the right of the crossover. We find that for any order
we fit the range of larger scales to the right of the crossover. We find that for any order  of the DFA-
of the DFA- method there are three regions with different relations between
method there are three regions with different relations between
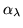 and
and  [Fig. 11(b)]:
[Fig. 11(b)]:
- (i)
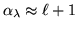 for
for
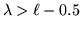 (region I);
(region I);
- (ii)
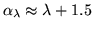 for
for
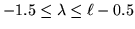 (region II);
(region II);
- (iii)
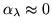 for
for 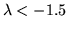 (region III).
(region III).
Note, that for integer values of the power  (
(
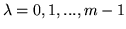 ), i.e. polynomial trends of order
), i.e. polynomial trends of order 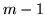 , the DFA-
, the DFA- method of order
method of order 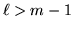 (
( is also an integer) leads to
is also an integer) leads to
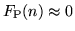 , since DFA-
, since DFA- is designed to remove polynomial trends. Thus for a integer values of the power
is designed to remove polynomial trends. Thus for a integer values of the power  there is no scaling and the effective exponent
there is no scaling and the effective exponent
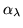 is not defined if a DFA-
is not defined if a DFA- method of order
method of order
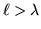 is used [Fig. 11]. However, it is of interest to examine the asymptotic behavior of the scaling of
is used [Fig. 11]. However, it is of interest to examine the asymptotic behavior of the scaling of  when the value of the power
when the value of the power  is close to an integer. In particular , we consider how the scaling of
is close to an integer. In particular , we consider how the scaling of  obtained from DFA-2 method changes when
obtained from DFA-2 method changes when
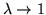 [Fig. 11(c)]. Surprisingly, we find that even though the values of
[Fig. 11(c)]. Surprisingly, we find that even though the values of  are very small at large scales, there is a scaling for
are very small at large scales, there is a scaling for  with a smooth convergence of the effective exponent
with a smooth convergence of the effective exponent
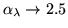 when
when
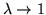 , according to the dependence
, according to the dependence
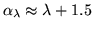 established for region II [Fig. 11(b)]. At smaller scales there is a flat region which is due to the fact that the fluctuation function
established for region II [Fig. 11(b)]. At smaller scales there is a flat region which is due to the fact that the fluctuation function 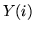 (Eq. (3)) is smaller than the precision of the numerical simulation.
(Eq. (3)) is smaller than the precision of the numerical simulation.



Next: Dependence of on the
Up: Noise with Power-law trends
Previous: Noise with Power-law trends
Zhi Chen
2002-08-28
