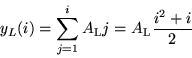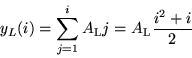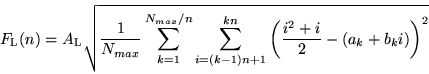Next: DFA-1 on Quadratic trend
Up: Appendix
Previous: Superposition law for DFA
DFA-1 on linear trend
 Let us suppose a linear time series
Let us suppose a linear time series
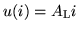 . The integrated signal
. The integrated signal 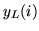 is
is
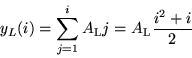 |
(32) |
Let as call  the size of the series and
the size of the series and  the size of the box. The rms fluctuation
the size of the box. The rms fluctuation 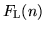 as a function of
as a function of  and
and  is
is
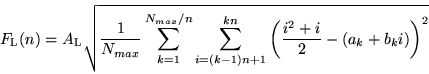 |
(33) |
where 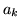 and
and 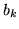 are the parameters of a least-squares fit of the
are the parameters of a least-squares fit of the 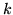 -th box of size
-th box of size  .
. 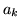 and
and 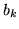 can be determined analytically,
thus giving:
can be determined analytically,
thus giving:
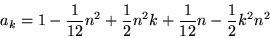 |
(34) |
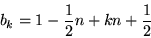 |
(35) |
With these values, 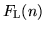 can be evaluated analytically:
can be evaluated analytically:
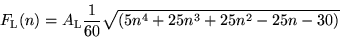 |
(36) |
The dominating term inside the square root is 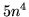 and then one obtains
and then one obtains
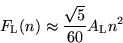 |
(37) |
leading directly to an exponent of 2 in the DFA. An important consequence is that, as 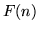 does not depend on
does not depend on  , for linear trends
with the same slope, the DFA must give exactly the same results
for series of different sizes. This is not
true for other trends, where the exponent is 2, but the factor
multiplying
, for linear trends
with the same slope, the DFA must give exactly the same results
for series of different sizes. This is not
true for other trends, where the exponent is 2, but the factor
multiplying 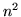 can depend on
can depend on  .
.



Next: DFA-1 on Quadratic trend
Up: Appendix
Previous: Superposition law for DFA
Zhi Chen
2002-08-28