


Next: Combined effect on of
Up: Noise with Power-law trends
Previous: Dependence of on the
Dependence of  on the signal length
on the signal length 
Here, we study how the rms fluctuation function  depends on the length
depends on the length  of the power-law signal
of the power-law signal
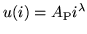 (
(
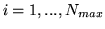 ). We find that there is a vertical shift in
). We find that there is a vertical shift in  with increasing
with increasing  [Fig. 13(a)]. We observe that when doubling the length
[Fig. 13(a)]. We observe that when doubling the length  of the signal the vertical shift in
of the signal the vertical shift in  , which we define as
, which we define as
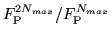 , remains the same, independent of the value of
, remains the same, independent of the value of  . This suggests a power-law dependence of
. This suggests a power-law dependence of  on the length of the signal:
on the length of the signal:
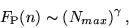 |
(21) |
where 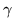 is an effective scaling exponent.
is an effective scaling exponent.
Next, we ask if the vertical shift depends on the power  of the power-law trend. When doubling the length
of the power-law trend. When doubling the length  of the signal, we find that for
of the signal, we find that for
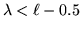 , where
, where  is the order of the DFA method, the vertical shift is a constant independent of
is the order of the DFA method, the vertical shift is a constant independent of  [Fig. 13(b)]. Since the value of the vertical shift when doubling the length
[Fig. 13(b)]. Since the value of the vertical shift when doubling the length  is
is 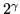 (from Eq. (21)), the results in Fig. 13(b) show that
(from Eq. (21)), the results in Fig. 13(b) show that 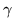 is independent of
is independent of  when
when
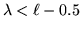 , and that
, and that
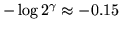 , i.e. the effective exponent
, i.e. the effective exponent
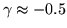 .
.
For
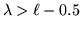 , when doubling the length
, when doubling the length  of the signal, we find that the vertical shift
of the signal, we find that the vertical shift 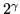 exhibits the following dependence on
exhibits the following dependence on  :
:
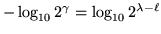 , and thus the effective exponent
, and thus the effective exponent 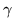 depends on
depends on  --
--
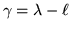 . For positive integer values of
. For positive integer values of  (
(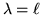 ), we find that
), we find that 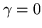 , and there is no shift in
, and there is no shift in  , suggesting that
, suggesting that  does not depend on the length
does not depend on the length  of the signal, when DFA of order
of the signal, when DFA of order  is used [Fig. 13]. Finally, we note that depending on the effective exponent
is used [Fig. 13]. Finally, we note that depending on the effective exponent 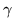 , i.e. on the order
, i.e. on the order  of the DFA method and the value of the power
of the DFA method and the value of the power  , the vertical shift in the rms fluctuation function
, the vertical shift in the rms fluctuation function  for power-law trend can be positive (
for power-law trend can be positive (
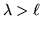 ), negative (
), negative (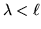 ), or zero (
), or zero (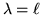 ).
).
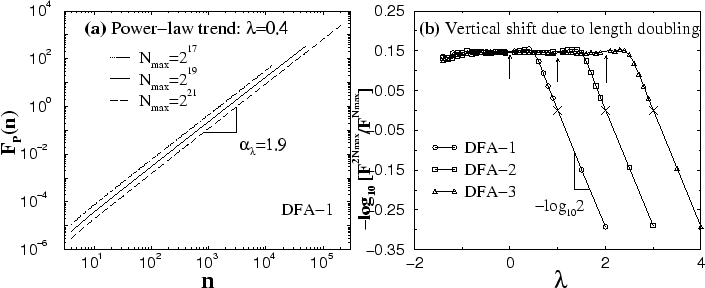
Figure 13:
Dependence of the rms fluctuation function 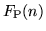 for power-law trend
for power-law trend
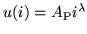 , where
, where
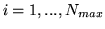 , on the length of the trend
, on the length of the trend  . (a) A vertical shift is observed in
. (a) A vertical shift is observed in 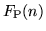 for different values of
for different values of  --
-- 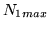 and
and 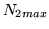 . The figure shows that the vertical shift , defined as
. The figure shows that the vertical shift , defined as
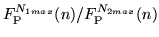 , does not depend on
, does not depend on  but only on the ratio
but only on the ratio
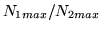 , suggesting that
, suggesting that
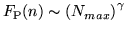 . (b) Dependence of the vertical shift on the power
. (b) Dependence of the vertical shift on the power  . For
. For
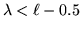 (
( is the order of DFA), we find a flat (constant) region characterized with effective exponent
is the order of DFA), we find a flat (constant) region characterized with effective exponent 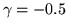 and negative vertical shift. For
and negative vertical shift. For
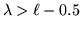 , we find an exponential dependence of the vertical shift on
, we find an exponential dependence of the vertical shift on  . In this region,
. In this region,
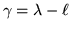 , and the vertical shift can be negative (if
, and the vertical shift can be negative (if 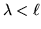 ) or positive (if
) or positive (if 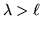 ). the slope of
). the slope of
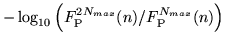 vs.
vs.  is
is 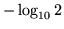 due to doubling the length of the signal
due to doubling the length of the signal  . This slope changes to
. This slope changes to 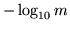 when
when  is increased
is increased 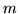 times while
times while 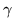 remains independent of
remains independent of  . For
. For 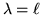 there is no vertical shift, as marked with
there is no vertical shift, as marked with 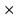 . Arrows indicate integer values of
. Arrows indicate integer values of 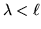 , for which values the DFA-
, for which values the DFA- method filters out completely the power-law trend and
method filters out completely the power-law trend and 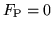 .
.
 |



Next: Combined effect on of
Up: Noise with Power-law trends
Previous: Dependence of on the
Zhi Chen
2002-08-28
