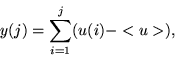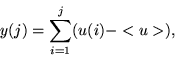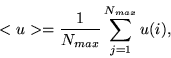Next: Noise with linear
trends Up: Effect
of Trends on Previous: Introduction
Method
To illustrate the DFA method, we consider a noisy time series, 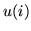 (
( 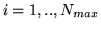 ). We integrate the time series
). We integrate the time series 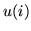 ,
,
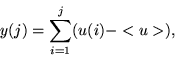 |
(1) |
where
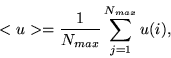 |
(2) |
and is divided into boxes of equal size,  . In each box, we
fit the integrated time series by using a polynomial function,
. In each box, we
fit the integrated time series by using a polynomial function, 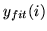 , which is called the local trend. For order-
, which is called the local trend. For order- DFA (DFA-1 if
DFA (DFA-1 if 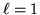 , DFA-2 if
, DFA-2 if 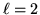 etc.),
etc.),  order polynomial function
should be applied for the fitting. We detrend The integrated time
series,
order polynomial function
should be applied for the fitting. We detrend The integrated time
series, 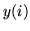 by subtracting the local trend
by subtracting the local trend 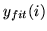 in each box, and we calculate the detrended
fluctuation function
in each box, and we calculate the detrended
fluctuation function
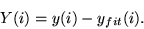 |
(3) |
For a given box size  , we calculate the root mean
square (rms) fluctuation
, we calculate the root mean
square (rms) fluctuation
![\begin{displaymath}
F(n) =\sqrt{\frac{1}{N_{max}}\sum\limits_{i=1}^{N_{max}}\left [Y(i)\right ]^2}
\end{displaymath}](img167.png) |
(4) |
The above computation is repeated for box sizes  (different scales) to provide a relationship between
(different scales) to provide a relationship between 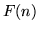 and
and  . A power-law relation between
. A power-law relation between 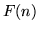 and the box
size
and the box
size  indicates the presence of scaling:
indicates the presence of scaling: 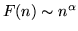 . The parameter
. The parameter 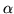 ,
called the scaling exponent or correlation exponent, represents the
correlation properties of the signal: if
,
called the scaling exponent or correlation exponent, represents the
correlation properties of the signal: if 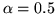 , there
is no correlation and the signal is an uncorrelated signal (white
noise); if
, there
is no correlation and the signal is an uncorrelated signal (white
noise); if 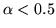 , the signal is anticorrelated;
if
, the signal is anticorrelated;
if 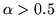 , there are positive
correlations in the signal.
, there are positive
correlations in the signal.



Next: Noise with linear
trends Up: Effect
of Trends on Previous: Introduction
Zhi Chen 2002-08-28