|
Part 1: Fractal
behavior in time series
The functions f(t) typically studied in mathematical analysis
are continuous and have continuous derivatives. Hence, they can be approximated
in the vicinity of some time ti by a so-called Taylor
series or power series
|
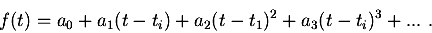 (eqn. 1) (eqn. 1) |
| For small regions around ti, just a few terms of the
expansion (eqn. 1) are necessary to approximate the function f(t). In
contrast, most time series f(t) found in "real-life" applications
appear quite noisy (Fig. 1). Therefore, at almost every point in
time, they cannot be approximated either by Taylor series (or by Fourier
series) of just a few terms. Moreover, many experimental or empirical
time series have fractal features--i.e., for some times ti,
the series f(t) displays singular behavior. By this, we
mean that at those times ti, the signal has components
with non-integer powers of time which appear as step-like or cusp-like
features, the so-called singularities, in the signal (see Figs. 1b,c).
|
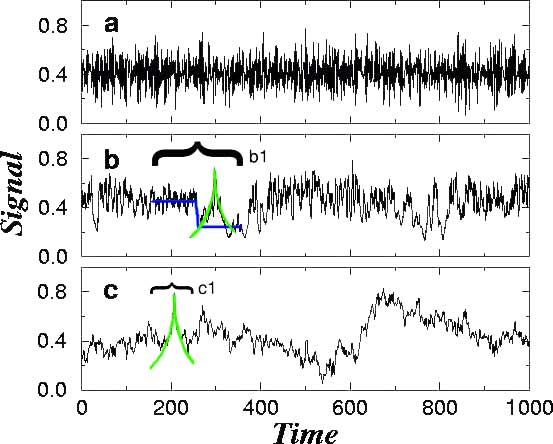 Figure 1: (a) A common example of
numerically-generated "noise" with long-range power-law correlations.
This signal has a power-law distributed power spectrum which increases
as (frequency)0.6. (b) Cardiac interbeat intervals
(in arbitrary units) for a healthy subject under ambulatory conditions.
Note that the interbeat intervals are plotted against beat number. It
is known that heart rate variability has long-range correlations characterized
by a power spectrum that decreases as (frequency)-1.0.
(c) Another example of numerically-generated noise also with long-range
correlations but of a different type. In this case, the power spectrum
decreases as (frequency)-1.4. Note how the high-frequency
features of the signal decrease from (a) to (c). Note also: plotted in
green are two instances of cusp-singularities (c1) and plotted
in blue (b1) is
one example of a step-singularity. Panel (b) also illustrates another
complicating factor in many instances, singularities are not isolated,
but may instead appear very close to one another, making their characterization
rather more complex.
Figure 1: (a) A common example of
numerically-generated "noise" with long-range power-law correlations.
This signal has a power-law distributed power spectrum which increases
as (frequency)0.6. (b) Cardiac interbeat intervals
(in arbitrary units) for a healthy subject under ambulatory conditions.
Note that the interbeat intervals are plotted against beat number. It
is known that heart rate variability has long-range correlations characterized
by a power spectrum that decreases as (frequency)-1.0.
(c) Another example of numerically-generated noise also with long-range
correlations but of a different type. In this case, the power spectrum
decreases as (frequency)-1.4. Note how the high-frequency
features of the signal decrease from (a) to (c). Note also: plotted in
green are two instances of cusp-singularities (c1) and plotted
in blue (b1) is
one example of a step-singularity. Panel (b) also illustrates another
complicating factor in many instances, singularities are not isolated,
but may instead appear very close to one another, making their characterization
rather more complex. |
Formally, one can write (2, 4): |
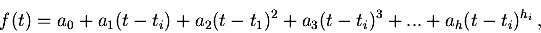 (eqn. 2) (eqn. 2) |
| where t is inside a small vicinity of ti, and
hi is a non-integer number quantifying the local singularity
of f(t) at t = ti. |
|
|
