


Next: DFA
Up: Effect of Trends on
Previous: Effect of Trends on
Many physical and biological systems exhibit complex behavior
characterized by long-range power-law correlations. Traditional
approaches such as the power-spectrum and correlation analysis are
not suited to accurately quantify long-range correlations in
non-stationary signals -- e.g. signals exhibiting fluctuations
along polynomial trends. Detrended fluctuation analysis
(DFA)[1,2,3,4] is a scaling analysis method
providing a simple quantitative parameter -- the scaling exponent
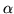 -- to represent the correlation properties of a signal.
The advantages of DFA over many methods are that it permits the detection of long-range correlations embedded in seemingly non-stationary time series, and also avoids the spurious detection of apparent long-range correlations that are artifact of non-stationarity. In the past few years, more than 100 publications have
utilized the DFA as method of correlation analysis, and have
uncovered long-range power-law correlations in many research
fields such as cardiac
dynamics[5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23],
bioinformatics[2,1,24,25,26,27,28,29,30,31,32,33,34],
economics[35,36,37,38,39,40,41,42,43,44,45,46,47],
meteorology[48,49,50],
material science[51], ethology[52] etc.
Furthermore, the DFA method may help identify different states of
the same system according to its different scaling behaviors --
e.g. the scaling exponent
-- to represent the correlation properties of a signal.
The advantages of DFA over many methods are that it permits the detection of long-range correlations embedded in seemingly non-stationary time series, and also avoids the spurious detection of apparent long-range correlations that are artifact of non-stationarity. In the past few years, more than 100 publications have
utilized the DFA as method of correlation analysis, and have
uncovered long-range power-law correlations in many research
fields such as cardiac
dynamics[5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23],
bioinformatics[2,1,24,25,26,27,28,29,30,31,32,33,34],
economics[35,36,37,38,39,40,41,42,43,44,45,46,47],
meteorology[48,49,50],
material science[51], ethology[52] etc.
Furthermore, the DFA method may help identify different states of
the same system according to its different scaling behaviors --
e.g. the scaling exponent 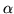 for heart inter-beat intervals
is different for healthy and sick
individuals[14,53,17,16].
for heart inter-beat intervals
is different for healthy and sick
individuals[14,53,17,16].
The correct interpretation of the scaling results obtained by the
DFA method is crucial for understanding the intrinsic dynamics of
the systems under study. In fact, for all systems where the DFA
method was applied, there are many issues that remain unexplained.
One of the common challenges is that the correlation exponent is
not always a constant (independent of scale) and crossovers often exist -- i.e. change
of the scaling exponent 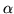 for different range of
scales[16,35,5]. A crossover
usually can arise from a change in the correlation
properties of the signal at different time or space scales, or can often arise from trends in the data. In
this paper, we systematically study how different types of trends
affect the apparent scaling behavior of long-range correlated signals.
The
existence of trends in times series generated by physical or
biological systems is so common that it is almost unavoidable. For
example, the number of particles emitted by a radiation source in
an unit time has a trend of decreasing because the source becomes
weaker[54,55]; the density of air due to gravity has a
trend at different altitude [56]; the
air temperature in different geographic locations and the water
flow of rivers have a periodic trend due to seasonal
changes[57,58,59,49,50]; the
occurrence rate of earthquakes in certain area has trend in
different time period[60]. An immediate problem
facing researchers applying scaling analysis to time series is
whether trends in data arise from external conditions, having
little to do with the intrinsic dynamics of the system generating
noisy fluctuating data. In this case, a possible approach is to
first recognize and filter out the trends before we attempt to
quantify correlations in the noise. Alternatively, trends may
arise from the intrinsic dynamics of the system, rather than being an
epiphenomenon of external conditions, and thus may be correlated
with the noisy fluctuations generated by the system. In this case,
careful considerations should be given if trends should be
filtered out when estimating correlations in the noise, since such
"intrinsic" trends may be related to the local properties of the
noisy fluctuations.
for different range of
scales[16,35,5]. A crossover
usually can arise from a change in the correlation
properties of the signal at different time or space scales, or can often arise from trends in the data. In
this paper, we systematically study how different types of trends
affect the apparent scaling behavior of long-range correlated signals.
The
existence of trends in times series generated by physical or
biological systems is so common that it is almost unavoidable. For
example, the number of particles emitted by a radiation source in
an unit time has a trend of decreasing because the source becomes
weaker[54,55]; the density of air due to gravity has a
trend at different altitude [56]; the
air temperature in different geographic locations and the water
flow of rivers have a periodic trend due to seasonal
changes[57,58,59,49,50]; the
occurrence rate of earthquakes in certain area has trend in
different time period[60]. An immediate problem
facing researchers applying scaling analysis to time series is
whether trends in data arise from external conditions, having
little to do with the intrinsic dynamics of the system generating
noisy fluctuating data. In this case, a possible approach is to
first recognize and filter out the trends before we attempt to
quantify correlations in the noise. Alternatively, trends may
arise from the intrinsic dynamics of the system, rather than being an
epiphenomenon of external conditions, and thus may be correlated
with the noisy fluctuations generated by the system. In this case,
careful considerations should be given if trends should be
filtered out when estimating correlations in the noise, since such
"intrinsic" trends may be related to the local properties of the
noisy fluctuations.
Here we study the origin and the properties of crossovers in the
scaling behavior of noisy signals, by applying the DFA method
first on correlated noise and then on noise with trends, and
comparing the difference in the scaling results. To this end, we
generate artificial time series -- anticorrelated, white and
correlated noise with standard deviation equal to one -- using
the modified Fourier filtering method introduced by Makse et
al.[63]. We consider the case when the trend is independent
of the local properties of the noise (external trend). We find
that the scaling behavior of noise with a trend is a superposition
of the scaling of the noise and the apparent scaling of the trend,
and we derive analytical relations based on the DFA, which we call
``superposition rule''. We show how this ``superposition rule'' can
be used to determine if the trends are independent of the noisy
fluctuation in real data, and if filtering these trends out will
no affect the scaling properties of the data.
The outline of this paper is as follows. In Sec.2, we
review the algorithm of the DFA method, and in Appendix
7.1 we compare the performance of the DFA with the
classical scaling analysis --Hurst's analysis (R/S analysis)--
and show that the DFA is a superior method to quantify the scaling
behavior of noisy signals. In Sec. 3, we consider the
effect of a linear trend and we present an analytic derivation of
the apparent scaling behavior of a linear trend in Appendix
7.3. In Sec. 4, we study a periodic trend,
and in Sec. 5 the effect of power-law trend. We
systematically study all resulting crossovers, their conditions of
existence and their typical characteristics associated with the
different types of trends. In addition, we also show how to use
DFA appropriately to minimize or even eliminate the effects of
those trends in cases that trends are not choices of the study,
that is, trends do not reflect the dynamics of the system but are
caused by some ``irrelevant'' background. Finally,
Sec. 6 contains a summary.



Next: DFA
Up: Effect of Trends on
Previous: Effect of Trends on
Zhi Chen
2002-08-28