ESTIMACIÓN ESPECTRAL:

    Una de las limitaciones de los métodos clásicos de estimación espectral de potencia reside en la estimación de la secuencia de autocorrelación. Para una secuencia de datos de longitud N, estos métodos pueden estimar la secuencia de autocorrelación únicamente para valores de retardo |k| < N, de manera que los valores correspondientes para |k| = N son puestos a cero. Puesto que muchas señales de interés poseen secuencias de autocorrelación no nulas para retardos superiores a N, este enventanado realizado por los métodos clásicos se traduce en una reducción de la resolución y de la exactitud de la estimación espectral. Estos métodos extrapolan la secuencia de autocorrelación con ceros, y lo que necesitamos para disminuir los efectos del enventanado es encontrar una extrapolación de la secuencia de autocorrelación más apropiada. EL Método de Máxima Entropía (MEM: Maximum Entropy Method) sugiere una vía alternativa para esta extrapolación.
 

    Supongamos que conocemos los valores de una secuencia de autocorrelación r_x(k) de un proceso aleatorio estacionario en sentido amplio (WSS) para retardos |k|<=p. En este punto, nuestro problema es la extrapolación de r_x(k) para |k|>p. A estos valores extrapolados los vamos a denotar como r_e(k).
    Es evidente que han de establecerse una serie de restricciones sobre r_e(k). Por ejemplo, si consideramos

 S_x(e^jw) debería corresponder a un espectro de potencia válido, es decir, S_x(e^jw) debería ser real y no negativo para todo w. Pero, en general, estas dos restricciones no son suficientes para garantizar una extrapolación única. Por tanto, debemos imponer restricciones adicionales a las posibles extrapolaciones. Una de estas restricciones, propuesta por Burg, consiste en calcular la extrapolación de manera que maximice la entropía del proceso. Como la entropía es una medida de aleatoriedad o incertidumbre, una extrapolación r_e(k) que cumpla esta condición de máxima entropía indica que el proceso x(n) ha sido lo más aleatorizado posible.

    Para un proceso aleatorio gaussiano con espectro de potencia S_x(e^jw), la entropía es

    Por tanto, para un proceso gaussiano del que se conoce una parte de la secuencia de autocorrelación, r_x(k) para |k|<=p, el espectro de potencia de máxima entropía es aquél que maximiza la ecuación anterior, y cumpla además que la transformada inversa de Fourier en tiempo discreto de  S_x(e^jw) sea igual a la secuencia dada de autocorrelación para |k|<=p,

    Los valores de r_e(k) que maximizan la entropía pueden obtenerse derivando H(x) respecto a r_e^*(k) e igualando a cero:

    De la expresión de S_x(e^jw) obtenemos que

y al sustituir en la derivada de H(x)

    Si definimos Q_x(e^jw) = 1/S_x(e^jw), la ecuación anterior refleja que la transformada inversa de Fourier en tiempo discreto es una secuencia de longitud finita que es igual a cero para valores |k|p,

      En consecuencia,

y de aquí obtenemos que el espectro de potencia de máxima entropía de un proceso gaussiano es un espectro de potencia todo-polos,

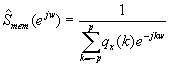
    Aplicando el teorema de factorización espectral, podemos expresar

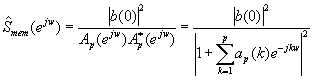
    Y en notación vectorial, con a_p = [1, a_p(1), ..., a_p(p)]^T y e = [1, e^jw, ..., e^jpw]^T, la estimación espectral MEM adquiere la forma

    Llegados a este punto, lo único que resta es encontrar los coeficientes a_p(k) y b(0). Debido a la restricción anteriormente aplicada, estos coeficientes deben ser elegidos de forma que la secuencia de autocorrelación obtenida al calcular la transformada inversa de Fourier del estimador, coincida con los valores dados de r_x(k) para |k|<=p. Si los coeficientes a_p(k) constituyen la solución de las ecuaciones normales:

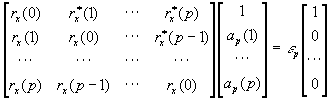
si consideramos

se satisface la restricción impuesta y el estimador MEM resulta

    Resumiendo, dada una secuencia de autocorrelación r_x(k) para k = 0, 1, ..., p, el estimador MEM resuelve las ecuaciones normales de autocorrelación y calcula los coeficientes a_p(k) y b(0). Posteriormente, incorpora estos parámetros en la ecuación anterior y obtiene la estimación espectral buscada.
    La expresión resultante del estimador de Máxima Entropía es un espectro de potencia de todo-polos, y, por tanto, r_x(k) satisface las ecuaciones de Yule-Walker

        ;     para l 0

    Por tanto, este método extrapola la secuencia de autocorrelación según esta recursión.
 
 

    Existe una interesante relación entre este método y el método MV, que afirma que la estimación MV de orden p es la media armónica de las estimaciones MEM de órdenes k = 0, 1, ..., p.

    Las propiedades de este método no están exentas de críticas y diversas interpretaciones. Podemos argumentar, por ejemplo, que en ausencia de información o restricciones sobre un proceso x(n), y dado un conjunto de valores de autocorrelación, r_x(0), r_x(1), ..., r_x(p), la mejor forma de estimar el espectro de potencia es calcular la transformada de Fourier de la secuencia de autocorrelación formada por los valores dados,  junto a una extrapolación obtenida con un criterio de máxima entropía. Este método debería ser preferible al impuesto por los métodos clásicos que asignan r_x(k) = 0, para |k|p. Por otro lado, dado que el método MEM utiliza un modelo de todo-polos para los datos, si el proceso no es consistente con este modelo, cabe esperar que los resultados obtenidos no sean muy exactos. Concluyendo, las prestaciones de este método, en comparación con el método de mínima varianza o con los métodos clásicos, dependen del tipo de proceso en cuestión y de la exactitud en el modelado AR de dicho proceso.
 

    Ejemplos

        1.- Estimación MEM de procesos AR y MA

    Componente Máxima Entropía