ESTIMACIÓN ESPECTRAL DE MÍNIMA VARIANZA
![]()
ESTIMACIÓN ESPECTRAL DE MÍNIMA VARIANZA
![]()
El método de estimación espectral de Mínima Varianza (MV: Minimun Variance), es una adaptación del Método de Máxima Verosimilitud (MLM: Maximum Likelihood Method), desarrollado por Capon para el análisis de densidades espectrales de potencia en dos dimensiones. En el método MV, la estimación del espectro se realiza filtrando un proceso con un banco de filtros paso-banda de banda estrecha.
En primer lugar, vamos a deducir la relación existente entre el proceso de salida filtrado yi(n) y el espectro de potencia que queremos estimar. Para ello, supondremos que x(n) es un proceso aleatorio estacionario en sentido amplio (WSS), con un espectro de potencia Sx(ejw), y que gi(n) es un filtro pasobanda ideal con un ancho de banda Dw y una frecuencia central wi,
![]()
Si filtramos x(n) con gi(n), el espectro de potencia del proceso de salida yi(n) es:
![]()
y la potencia de yi(n)
![]()
Si el ancho de banda Dw es lo suficientemente pequeño, podremos considerar que Sx(ejw) es aproximadamente constante en la banda de paso del filtro, por lo que la potencia anterior se aproxima
![]()
Por tanto, es posible estimar la densidad espectral de potencia de x(n) en la frecuencia w = wi, a partir del proceso filtrado, estimando la potencia en yi(n) y dividiendo por el ancho de banda normalizado del filtro, Dw/2p,
![]()
El periodograma produce una estimación del espectro en una forma similar. En concreto, x(n) es filtrado con un banco de filtros pasobanda, hi(n), donde
![]()
y la potencia en cada una de las señales filtradas es estimada utilizando un promedio de una sola muestra,
![]()
El periodograma, por tanto, se forma dividiendo la estimación de potencia por el ancho del filtro Dw=2p/N. Como los filtros que componen el banco de filtros son iguales, y difieren únicamente en la frecuencia central, estos filtros son independientes de los datos. En consecuencia, cuando un proceso aleatorio contiene una cantidad significativa de potencia en bandas frecuenciales dentro de los lóbulos laterales de la banda de paso del filtro, se producen pérdidas a través de estos lóbulos que provocan una distorsión en la estimación del espectro.
Una manera mejor de realizar la estimación consiste en permitir que cada filtro en el banco de filtros sea adaptativo, dependiente de los datos, de forma que cada filtro se diseñe con el objetivo de ser "óptimo", en el sentido de rechazar la máxima potencia de señal fuera de la banda. La técnica MV se basa en esta idea, y básicamente, sigue estos pasos:
Vamos a obtener el estimador de espectro MV. Para ello, comenzamos con el diseño del banco de filtros pasobanda.
Supongamos que queremos estimar la densidad espectral de potencia de x(n) en la frecuencia wi, y que gi(n) es un filtro paso-banda FIR de oden p y valores complejos. Para asegurar que el filtro no altera la potencia en el proceso de entrada a la frecuencia wi, vamos a imponer la restricción sobre Gi(ejw) de tener ganancia unidad en w = wi,
![]()
que en forma vectorial puede ser expresado
![]()
donde gi es el vector de coeficientes del filtro gi(n),
![]()
y ei el vector de exponenciales complejas ejkwi,
![]()
Para asegurar que el espectro de potencia de x(n) a la frecuencia wi sea medido de la forma más precisa posible, el filtro paso-banda debe rechazar el máximo de potencia en las demás frecuencias. Por tanto, el criterio de diseño va a ser minimizar la potencia del proceso de salida sujeto a la restricción de ganancia unidad en la frecuencia central del filtro. Como la potencia en yi(n) puede ser expresada en términos de la matriz de autocorrelación Rx,
![]()
el problema se reduce a minimizar la ecuación anterior con la restricción comentada. Podemos definir una función de coste que refleje esta operación
![]()
Derivando e igualando a cero, hallamos la solución gi = l Rx-1ei , donde l = 1 / (ei HRx-1ei ). Por tanto, el vector de coeficientes del filtro es
![]()
donde el mínimo valor de E{|yi(n)|2} es
![]()
Esta ecuación define la potencia en yi(n), que es utilizada como la estimación de la potencia de x(n) a la frecuencia wi. Tanto esta ecuación como la anterior, han sido derivadas para una frecuencia específica, wi, y dado que esta frecuencia es arbitraria, podemos considerar estas ecuaciones válidas para toda w. En consecuencia, el filtro óptimo para la estimación de la potencia a la frecuencia w es
![]()
y la estimación de potencia
![]()
donde e = [1, ejw, ..., ejpw]T.
Una vez diseñado el banco de filtros y estimada la distribución de potencia de x(n) como una función de la frecuencia, ahora podríamos estimar el espectro de potencia dividiendo la potencia estimada entre el ancho de banda del filtro. Aunque existen diferentes criterios que definen el ancho de banda, lo más sencillo es utilizar el valor de D que produce la densidad espectral correcta para ruido blanco. Como la estimación MV de potencia en ruido blanco es E{|yi(n)|2} = sx2 /(p+1), la estimación del espectro es
![]()
Por tanto, si consideramos
![]()
entonces, la estimación del espectro es simplemente sx2. Si utilizamos la expresión anterior de D como el ancho de banda del filtro g(n), la estimación espectral de potencia se convierte en
![]()
que es el estimador espectral de mínima varianza. Observamos que está definido en términos de la matriz de autocorrelación Rx de x(n). En caso de que esta matriz sea desconocida, puede sustituirse por una matriz de autocorrelación estimada.
Podemos obtener una expresión alternativa que evite realizar la inversa de la matriz de autocorrelación Rx (o de la matriz de autocorrelación estimada).
Comenzamos descomponiendo la matriz Rx en términos de la matriz de autovectores Q y la matriz de autovalores L. Suponemos que cada autovector de la matriz de autovectores se denota por fi ( i = 1, 2, ..., p+1):
![]()
y la inversa de la matriz Rx es
![]()
A partir de la expresión del estimador de mínima varianza
![]()
y con la relación
![]()
obtenemos la siguiente ecuación para el estimador
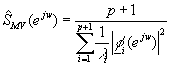
que ya no requiere la inversión de la matriz de autocorrelación, y trabaja directamente con los autovectores (calculando sus transformadas de Fourier) y con los autovalores.
Orden del filtro p
Un asunto importante en este capítulo es la elección del orden del filtro, p. Claramente, debe ser alto para que el filtro rechace mejor la potencia fuera de banda, y con ello ofrezca una buena resolución. Pero, en la práctica, existe un límite para este valor. Con un filtro de orden p, el estimador MV requiere evaluar la inversa de una matriz de autocorrelación de dimensiones (p+1) X (p+1). Para calcular la inversa, es necesario conocer los valores de rx(k) para k = 0, 1, ..., N-1. Por tanto, el orden se encuentra limitado a p <= N. De todas formas, el orden del filtro generalmente es mucho menor que este valor máximo, debido a que la varianza se incrementa al subir p y acercarse a N.
Contamos, por tanto, con el compromiso resolución - varianza.
Variantes al método MV
Exiten otras formas de estimar el espectro por el método de Mínima Varianza que discrepan de la anterior en la manera en que el filtro es diseñado o en el modo de evaluar la potencia en la señal de salida.
Por ejemplo, en el algoritmo DASE (Data Adaptive Spectrum Estimation), la restricción aplicada a Gi(ejw) consiste en limitar la energía a la unidad en una banda de paso de anchura Dw centrada en la frecuencia wi,
![]()
![]()
Ejemplos
1.- Método de Mínima Varianza y Máxima Entropía
![]()
![]()