MÁXIMA ENTROPÍA - MÍNIMA VARIANZA

    Vamos a demostrar que la estimación MV de orden p es la media armónica de las estimaciones MEM de los órdenes
k = 0, 1 , ...,  p. Para ello, utilizaremos la recursión que permite expresar la inversa de una matriz Toeplitz R_p de dimensiones (p+1) x (p+1) según

    Para un proceso aleatorio estacionario en sentido amplio (WSS) con una matriz de autocorrelación R_p, la estimación MV de orden p es

    Multiplicando R_p^-1 por e^H por la izquierda y por e por la derecha, obtenemos

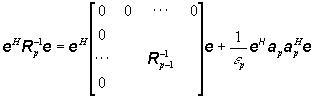
y utilizando notación vectorial

    Observamos que los dos primeros términos son proporcionales a la inversa de las estimaciones MV de órdenes p y p-1, respectivamente. El último término, por su parte, es la inversa de la estimación MEM de orden p. Por tanto,

notamos que es una recursión de la estimación MV de orden p en términos de la estimación MV de orden (p-1) y del espectro MEM de orden p. Si resolvemos la recursión para encontramos la relación

    La estimación MV es la media armónica de las estimaciones MEM desde el menor hasta el mayor orden de estimación. Como resultado de este promedio (y, en consecuencia, suavizado), para un proceso WSS formado por componentes de banda estrecha en ruido, el método MEM ofrecerá una mayor resolución en la estimación espectral que el método MV.