Algoritmo LMS
![]()
Algoritmo LMS
(Least-Mean-Square)
![]()
El algoritmo LMS pertenece a la familia de los algoritmos de gradiente estocástico. Con el término "estocástico" se pretende distinguir este algoritmo del Steepest Descent, que utiliza un gradiente determinista para el cálculo de los coeficientes del filtro.
Una característica importante del LMS es su simplicidad. No requiere medidas de las funciones de correlación, ni tampoco inversión de la matriz de autocorrelación.
El LMS comprende dos procesos básicos:
Si fuera posible obtener medidas exactas del vector gradiente Ñx(n) en cada iteración n, y dispusiéramos del parámetro m adecuadamente elegido, el vector de pesos del filtro convergería a la solución óptima de Wiener. Pero en la realidad no disponemos de estas medidas exactas del vector gradiente, ya que no conocemos la matriz de autocorrelación de la señal de entrada al filtro ni el vector de correlación cruzada entre esta señal de entrada al filtro y la respuesta deseada. Por tanto, el vector gradiente ha de ser estimado a partir de los datos.
La manera más sencilla de estimar el vector gradiente consiste en sustituir en la expresión
Ñx(n) = -2 p + 2 R w(n)
R y p por estimaciones instantáneas constituidas por los valores de señal de entrada al filtro y por la respuesta deseada,
![]()
![]()
Y obtenemos así una estimación instantánea del vector gradiente
![]()
Esta estimación puede verse como el resultado de aplicar el operador gradiente Ñ al error instantáneo |e(n)|2. Si sustituimos la estimación del vector gradiente en la ecuación de actualización de los pesos utilizada en el algoritmo Steepest-Descent
{ w(n+1) = w(n) - (1/2) m (-Ñx(n)) } obtenemos la relación recursiva siguiente:
![]()
Podemos expresar esta solución con las relaciones siguientes:
En cada iteración, la actualización de un peso requiere dos multiplicaciones complejas y una suma. Por tanto, para un filtro de p coeficientes, se realizan 2p+1 multiplicaciones complejas y 2p sumas complejas por iteración. Es decir, la carga computacional es del orden de p ( O(p) ).
Observamos que la estimación del error, definida por las ecuaciones 1 y 2, depende del vector de pesos actual w(n), y el término m x(n) e*(n) representa la corrección aplicada al vector de pesos w(n). El algoritmo iterativo ha de comenzar con un valor inicial w(0). También notamos que en cada iteración se debe conocer el valor de x(n), d(n) y w(n).
Cuando este algoritmo de gradiente estocástico opera con señales estocásticas, las direcciones del gradiente son aleatorias y generalmente no coinciden con la dirección señalada por el Steepest-Descent. Pero, al ser no sesgado en media, la corrección aplicada al vector de pesos sigue, en media, la dirección del Steepest-Descent.
![]()
![]()
Puesto que el vector w(n) se compone de variables aleatorias, para estudiar la convergencia del algoritmo, debemos trabajar dentro de un marco estadístico y bajo la suposición de independencia.
Partimos de la ecuación de actualización de los pesos del filtro,
![]()
y aplicamos el valor esperado; así, obtenemos:
E[w(n+1)] = E[w(n)] + mE[x(n)d*(n)] - mE[x(n)xH(n)w(n)]
(con la suposición de independencia)
E[w(n+1)] = E[w(n)] + mE[x(n)d*(n)] - mE[x(n)xH(n)] E[w(n)]
E[w(n+1)] = E[w(n)] + mp - m R E[w(n)]
E[w(n+1)] = (I - m R )E[w(n)] + m p
E[w(n+1)] = (I - m R )E[w(n)] + mR wopt
Obtenemos, por tanto, la misma ecuación que en el algoritmo Steepest-Descent, pero en este caso con valor esperado. Y podemos realizar el mismo proceso para deducir la condición de estabilidad. De esta forma, definimos el mismo vector de traslación al punto óptimo c(n) como
c(n) = w(n) - wopt
Descomponiendo la matriz R en función de sus autovalores y autovectores (R = Q LQH ) y aplicando la rotación para obtener los autovectores como ejes de representación, llegamos a
E[v(n)] = (I - mL)n E[v(0)] o E[v(n)] = (I - mL)n v(0)
donde v(0) es el valor incial del vector de pesos en los ejes principales del sistema.
m debe cumplir la misma condición que en el algoritmo Steepest-Descent, es decir
![]()
donde lmax es el mayor autovalor de la matriz de autocorrelación. Este límite asegura la convergencia en media, pero no impone restricciones en la varianza. Es decir, cumpliéndose la condición anterior, el sistema puede converger en media pero no en varianza. Además, para obtener lmax la matriz R debe ser conocida. Para evitar este problema, podemos utilizar:
![]()
Si la señal x(n) es estacionaria en sentido amplio, R es Toeplitz, y para p coeficientes,
![]()
Y así obtenemos la condición de convergencia en media
![]()
![]()
La potencia de señal podría ser estimada mediante un promediado
![]()
Con el fin de asegurar la convergencia en varianza, el parámetro m debe elegirse de forma más restrictiva:
![]()
Cuando el vector de pesos comienza a converger en media, los coeficientes empiezan a fluctuar en torno a sus valores óptimos. Estas fluctuaciones son debidas a que el vector gradiente utilizado para realizar las correcciones al vector de pesos es ruidoso. En consecuencia, la varianza del error no tiende a cero y el error cuadrático medio es mayor que el error cuadrático medio mínimo en una cantidad denominada exceso de error cuadrático medio. Para determinar este exceso de error, comenzamos escribiendo el error en el instante n de la forma siguiente:
e(n) = d(n) - wH(n) x(n) = d(n) - woptHx(n) - cH(n) x(n) = emin(n) - cH(n) x(n)
donde emin(n) es el error correspondiente al vector de pesos óptimo, es decir,
emin(n) = d(n) - woptHx(n)
Suponiendo que el filtro se encuentra en estado estacionario, E[c(n)] = 0, y el error cuadrático medio puede ser expresado como
x(n) = E[|e(n)|2] = xmin + xex(n)
donde xmin = E[|emin(n)|2] es el mínimo error cuadrático medio y xex(n) es el exceso de error cuadrático medio, que depende de las estadísticas de x(n), c(n) y d(n). Asumiendo la condición de independencia, podemos llegar a la siguiente propiedad del LMS:
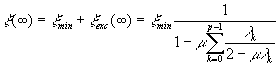
y el algoritmo converge en sentido cuadrático medio si el paso de convergencia m satisface las condiciones:
![]()
![]()
Si se cumple m << 2/lk, esta última ecuación puede simplificarse a
![]()
o,
![]()
Y cuando m << 2/lmax se puede expresar
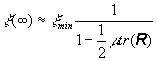
El exceso de error cuadrático medio es
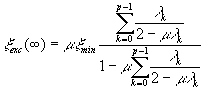
y con las simplificaciones anteriores se convierte en
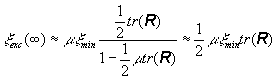
Obervamos que para valores pequeños de m, el exceso de error cuadrático medio es proporcional al parámetro m. Los filtros adaptativos pueden ser descritos en términos de su desajuste, un error cuadrático medio normalizado, definido como la relación entre el exceso de error cuadrático medio en el estado estacionario y el mínimo error cuadrático medio:
![]()
que valores pequeños de m, m << 2/lmax, puede escribirse como
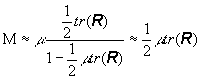
![]()
1.- Filtrado LMS en proceso AR(2)
2.- Estudio del error cuadrático medio
![]()