Ejemplo 1.- Filtrado LMS.

Consideremos un proceso AR(2) generado según la ecuación

x(n) = v(n) + 1.2728 x(n-1) - 0.81 x(n-2)

donde v(n) es ruido blanco gaussiano de varianza unidad.

El predictor lineal causal óptimo para x(n) viene dado por la ecuación

Para diseñar este predictor (es decir, para saber que los coeficientes óptimos del predictor son 1.2728 y -0.81), se ha de conocer la secuencia de autocorrelación de x(n). Por tanto, vamos a considerar un predictor lineal adaptativo de la forma

donde los coeficientes se actualizan de la siguiente manera:

w_k(n+1) = w_k(n) + m x(n-k) e*(n)

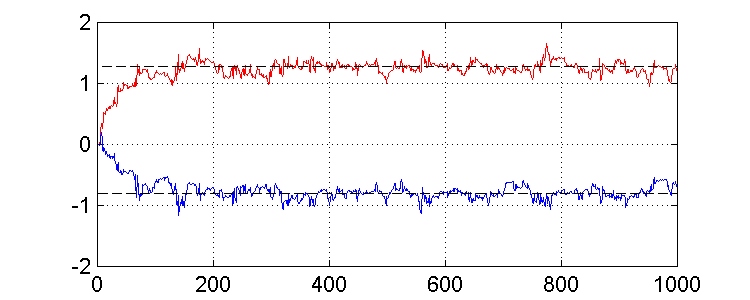
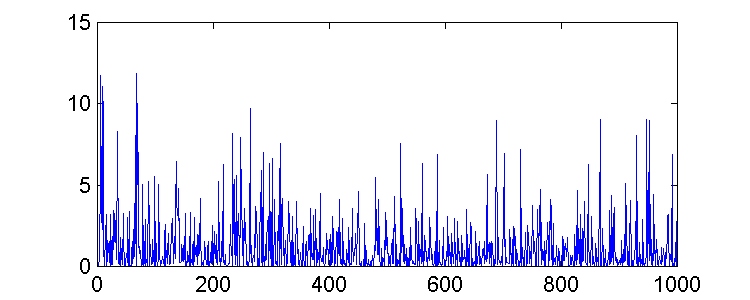
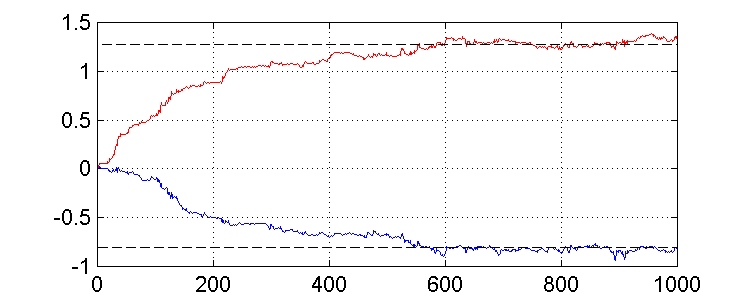
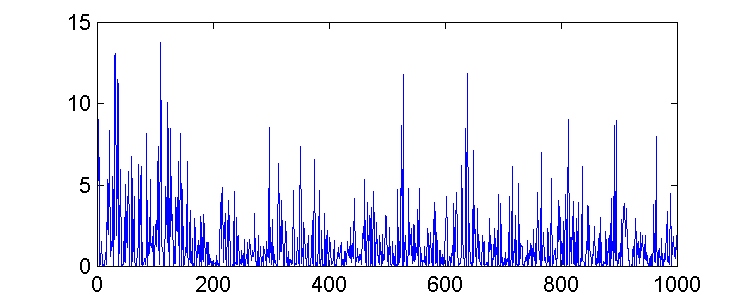
Si el valor del paso de convergencia m es suficientemente pequeño, los coeficientes w₁(n) y w₂(n) convergerán en media a sus valores óptimos, 1.2728 y -0.81, respectivamente. El error de predicción es

Por consiguiente, cuando w₁(n) = 1.2728 y w₂(n) = -0.81, el error pasa a ser v(n), y el mínimo error ecuadrático medio es

x_min = s_v² = 1

pero, aunque podríamos esperar que el error cuadrático medio convergiera a x_min según el vector de pesos converge a los valores óptimos, esto no ocurre así. Existe una gran variación en los valores del error, como podemos observar en las gráficas.

Comenzamos el algoritmo con un vector de pesos inicializado a cero ( w(0) = 0 ), y consideramos dos valores diferentes de m (0.02 y 0.004).

m = 0.02
La primera gráfica corresponde a la evolución de los coeficientes. Observamos que, aunque convergen relativamente pronto, existe una gran fluctuación en torno a los valores óptimos. El error presenta una gran variación si lo comparamos con el que obtendríamos con el algoritmo Steepest-Descent. No debemos olvidar que ahora trabajamos con un gradiente instantáneo.

m = 0.004
En este caso, la convergencia de los pesos es más lenta, pero la fluctuación es menor y los coeficientes se aproximan con mayor exactitud a los valores óptimos. Observamos, por tanto, la relación entre los factores velocidad de convergencia, estabilidad y varianza, establecida por m. Con un valor de m menor, (suponemos convergencia garantizada), la convergencia es más lenta y los coeficientes necesitan más iteraciones para aproximarse a los valores deseados; este camino hacia los valores óptimos también se realiza de manera más suave, sin tantas fluctuaciones, hasta alcanzar unos valores más cercanos a los óptimos.