Volver al LMS

    Ejemplo 2.- Estudio del error cuadrático medio en el filtrado LMS.

    Consideremos el proceso AR(2) del ejemplo anterior, generado según la ecuación

donde v(n) es ruido blanco gaussiano de varianza unidad.
 

    Vamos a evaluar el error cuadrático medio para distintos pasos de convergencia y compararemos los resultados experimentales obtenidos con los teóricos.

    Puesto que la curva de aprendizaje es una representación de x(n) = E{|e(n)|²}frente a n, podemos aproximar esta curva de aprendizaje promediando los valores de |e(n)|² obtenidos en distintas realizaciones. Supongamos que implementamos el predictor K veces, y en cada realización k tenemos el error cuadrático en el instante n denotado por  |e_k(n)|². Así tenemos

    En concreto elegimos  K = 200, y un vector de pesos inicializado a cero. Elegimos los valores de paso de convergencia del ejemplo anterior ( m = 0.02  y m = 0.004).

    Obtenemos las siguientes estimaciones de error cuadrático medio:

• m = 0.02:

• m = 0.004:

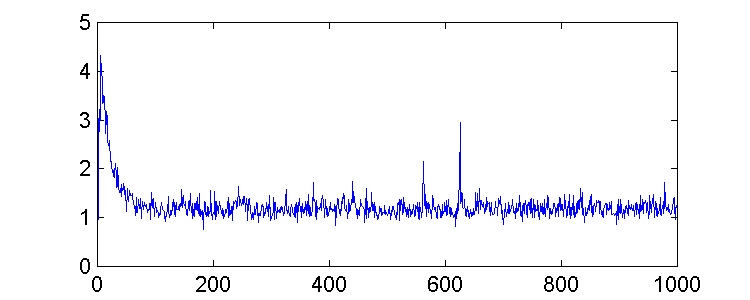
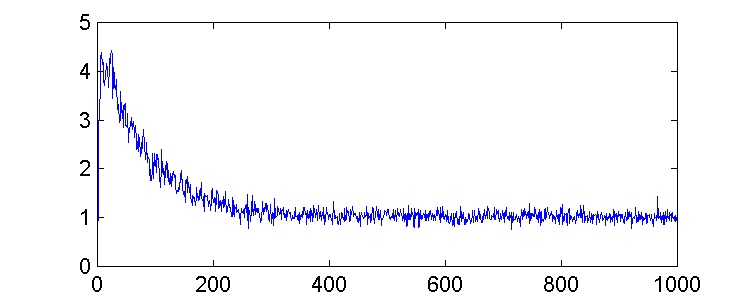
    Podemos observar que un valor de m menor implica una convergencia hacia el estacionario más lenta, pero el error cuadrático medio es menor. Estos efectos se aprecian mejor en la gráfica siguiente, en la que aparecen las dos curvas superpuestas (en rojo, la correspondiente a m = 0.02, y en azul; m = 0.004).

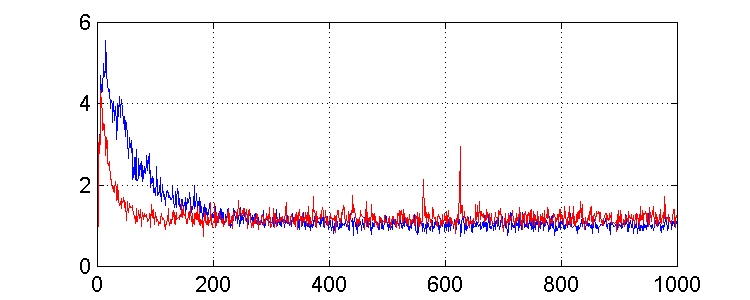
    Para estimar el error cuadrático medio en la convergencia debemos promediar el resultado obtenido cuando el algoritmo ha alcanzado el estado estacionario. Podemos elegir las 100 últimas muestras:

    Y asi, obtenemos que el error cuadrático medio x(n) obtenido en el estacionario es:

• 1.1988 ;  para  m = 0.02;
• 1.0219 ;  para  m = 0.004;

    Si comparamos estos valores con los teóricos, a partir de la ecuación

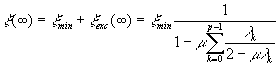
y teniendo en cuenta que x_min = 1, y los autovalores toman los valores l₁ = 9.7924  y   l₂ = 1.7073, obtenemos

• 1.1442 ;  para  m = 0.02;
• 1.0240 ;  para  m = 0.004;

valores cercanos a los estimados.