Dependence on the size of segments

Next, we study how the scaling behavior of the components depends on the size of the segments $W$.

First, we consider components containing segments with anti-correlations. For a fixed value of the fraction $p$ of the segments, we study how $F(n)/n$ changes with $W$. At small scales, we observe a behavior with a slope similar to the one for a stationary signal $u(i)$ with identical anti-correlations [Fig. 8(a)]. At large scales, we observe a crossover to random behavior (exponent $\alpha =0.5$) with an increasing crossover scale when $W$ increases. At large scales, we also find a vertical shift with increasing values for $F(n)/n$ when $W$ decreases [Fig. 8(a)]. Moreover, we find that there is an equidistant vertical shift in $F(n)/n$ when $W$ decreases by a factor of ten, suggesting a power-law relation between $F(n)/n$ and $W$ at large scales.

Figure 8: Dependence of the scaling behavior of components on the segment size $W$. The fraction $p=0.1$ of the non-zero segments is fixed and the length of the components is $N_{max}=2^{20}$. (a) Components containing anti-correlated segments ($\alpha =0.1$). At large scales ($n\gg W$), there is a crossover to random behavior ($\alpha =0.5$). An equidistant vertical shift in $F(n)/n$ when $W$ decreases by a factor of ten suggests a power-law relation between $F(n)/n$ and $W$. (b) Components containing correlated segments ($\alpha =0.9$). At intermediate scales, $F(n)/n$ has slope $\alpha =0.5$, indicating random behavior. An equidistant vertical shift in $F(n)/n$ suggests a power-law relation between $F(n)/n$ and $W$.

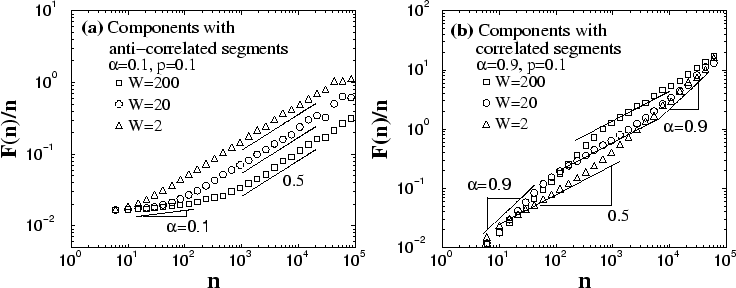For components containing correlated segments with a fixed value of the fraction $p$ we find that in the intermediate scale regime, the segment size $W$ plays an important role in the scaling behavior of $F(n)/n$ [Fig. 8(b)]. We first focus on the intermediate scale regime when both $p=0.1$ and $W=20$ are fixed [middle curve in Fig. 8(b)]. We find that for a small fraction $p$ of the correlated segments, $F(n)/n$ has slope $\alpha =0.5$, indicating random behavior [Fig. 8(b)] which shrinks when $p$ increases [see Appendix 7.2, Fig. 10]. Thus, for components containing correlated segments, $F(n)/n$ approximates at large and small scales the behavior of a stationary signal with identical correlations ($\alpha =0.9$), while in the intermediate scale regime there is a plateau of random behavior due to the random ``jumps'' at the borders between the non-zero and zero segments [Fig. 5(c)]. Next, we consider the case when the fraction of correlated segments $p$ is fixed while the segment size $W$ changes. We find a vertical shift with increasing values for $F(n)/n$ when $W$ increases [Fig. 8(b)], opposite to what we observe for components with anti-correlated segments [Fig. 8(a)]. Since the vertical shift in $F(n)/n$ is equidistant when $W$ increases by a factor of ten, our finding indicates a power-law relationship between $F(n)/n$ and $W$.