Strongly correlated segments

For components containing segments with stronger positive correlations ($\alpha>1$) and fixed $W=20$, we find that at small scales ($n<W$), the slope of $F(n)/n$ does not depend on the fraction $p$ and is close to that expected for a stationary signal $u(i)$ with identical correlations (Fig. 10). Surprisingly we find that in order to collapse the $F(n)/n$ curves obtained for different values of the fraction $p$, we need to rescale $F(n)/n$ by $\sqrt {p(1-p)}$ instead of $\sqrt {p}$, which is the rescaling factor at small scales for components containing segments with correlations $\alpha<1$. Thus $\alpha=1$ is a threshold indicating when the rescaling factor changes. Our simulations show that this threshold increases when the segment size $W$ increases.
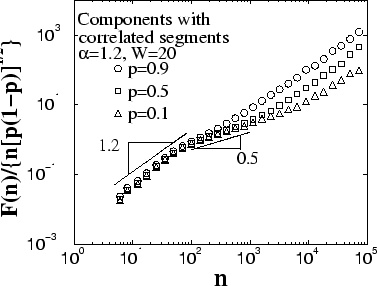
For components containing a sufficiently small fraction $p$ of correlated segments ($\alpha >0.5$), we find that in the intermediate scale regime there is a crossover to random behavior with slope $0.5$. The $F(n)/n$ curves obtained for different values of $p$ collapse in the intermediate scale regime if we rescale $F(n)/n$ by $\sqrt {p(1-p)}$ (Fig. 10). We note that this random behavior regime at intermediate scales shrinks with increasing the fraction $p$ of correlated segments and, as expected, for $p$ close to $1$ this regime disappears (see the $p=0.9$ curve in Fig. 10).

Figure 10: Dependence of the scaling behavior of components on the fraction $p$ of the segments with strong positive correlations ($\alpha =1.2$). The segment size is $W=20$ and the length of the components is $N_{max}=2^{20}$. After rescaling $F(n)/n$ by $\sqrt {p(1-p)}$, all curves collapse at small scales ($n<W$) with slope $1.2$ and at intermediate scales with slope $0.5$. The intermediate scale regime shrinks when $p$ increases.