For components containing segments with anti-correlations (
First, we study how the correlation properties of the components depend on
the fraction ![]() of the segments with identical local correlations.
of the segments with identical local correlations.
For components containing segments with anti-correlations (![]() )
and fixed size
)
and fixed size ![]() [Fig. 5(b)], we find a crossover to random behavior (
[Fig. 5(b)], we find a crossover to random behavior (![]() ) at
large scales, which becomes more pronounced (shift to smaller scales) when
the fraction
) at
large scales, which becomes more pronounced (shift to smaller scales) when
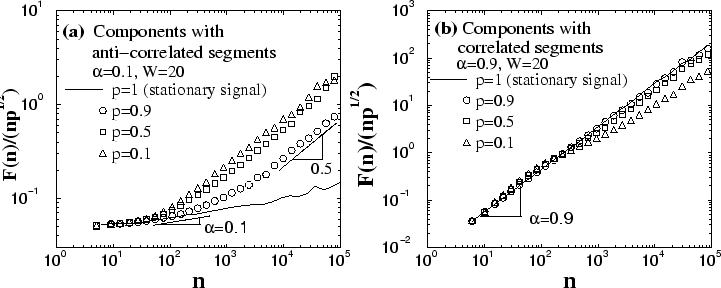
the fraction ![]() decreases [Fig. 6(a)]. At small scales
(
decreases [Fig. 6(a)]. At small scales
(![]() ), the slope of
), the slope of
![]() is identical to that expected for a stationary signal
is identical to that expected for a stationary signal ![]() (i.e.,
(i.e., ![]() ) with the same anti-correlations [solid line in
Fig. 6(a)]. Moreover, we observe a vertical shift in
) with the same anti-correlations [solid line in
Fig. 6(a)]. Moreover, we observe a vertical shift in ![]() to
lower values when the fraction
to
lower values when the fraction ![]() of non-zero anti-correlated segments
decreases. We find that at small scales after rescaling
of non-zero anti-correlated segments
decreases. We find that at small scales after rescaling ![]() by
by
![]() , all curves collapse on the curve for the stationary
anti-correlated signal
, all curves collapse on the curve for the stationary
anti-correlated signal ![]() [Fig. 6(a)]. Since at small scales
(
[Fig. 6(a)]. Since at small scales
(![]() ) the behavior of
) the behavior of ![]() does not depend on the segment size
does not depend on the segment size ![]() ,
this collapse indicates that the vertical shift in
,
this collapse indicates that the vertical shift in ![]() is due only to
the fraction
is due only to
the fraction ![]() . Thus, to determine the fraction
. Thus, to determine the fraction ![]() of anti-correlated
segments in a nonstationary signal [mixture of anti-correlated and correlated
segments, Fig. 5(a)] we only need to estimate at small scales the
vertical shift in
of anti-correlated
segments in a nonstationary signal [mixture of anti-correlated and correlated
segments, Fig. 5(a)] we only need to estimate at small scales the
vertical shift in ![]() between the mixed signal [Fig. 5(d)] and a stationary signal
between the mixed signal [Fig. 5(d)] and a stationary signal ![]() with identical anti-correlations. This approach is valid for
nonstationary signals where the fraction
with identical anti-correlations. This approach is valid for
nonstationary signals where the fraction ![]() of the anti-correlated
segments is much larger than the fraction of the correlated segments in the
mixed signal [Fig. 5(a)], since only under this condition the
anti-correlated segments can dominate
of the anti-correlated
segments is much larger than the fraction of the correlated segments in the
mixed signal [Fig. 5(a)], since only under this condition the
anti-correlated segments can dominate ![]() of the mixed signal at small
scales [Fig. 5(d)].
of the mixed signal at small
scales [Fig. 5(d)].
 |
For components containing segments with positive correlations
(![]() ) and fixed size
) and fixed size ![]() [Fig. 5(c)], we observe a similar behavior for
[Fig. 5(c)], we observe a similar behavior for ![]() , with collapse
at small scales (
, with collapse
at small scales (![]() ) after rescaling by
) after rescaling by ![]() [Fig. 6(b)] (For
[Fig. 6(b)] (For ![]() , there are
exceptions with different rescaling factors, see
Appendix 7.2). At small scales the values of
, there are
exceptions with different rescaling factors, see
Appendix 7.2). At small scales the values of ![]() for
components containing segments with positive correlations are
much larger compared to the values of
for
components containing segments with positive correlations are
much larger compared to the values of ![]() for components containing an
identical fraction
for components containing an
identical fraction ![]() of anti-correlated segments
[Fig. 6(a)]. Thus, for a mixed signal where the fraction of
correlated segments is not too small (e.g.,
of anti-correlated segments
[Fig. 6(a)]. Thus, for a mixed signal where the fraction of
correlated segments is not too small (e.g., ![]() ), the contribution at
small scales of the anti-correlated segments to
), the contribution at
small scales of the anti-correlated segments to ![]() of the
mixed signal [Fig. 5(d)] may not be observed, and the behavior (values
and slope) of
of the
mixed signal [Fig. 5(d)] may not be observed, and the behavior (values
and slope) of ![]() will be dominated by the correlated segments. In this
case, we must consider the behavior of
will be dominated by the correlated segments. In this
case, we must consider the behavior of ![]() of the mixed signal at
large scales only, since the contribution of the anti-correlated segments at
large scales is negligible. Hence, we next study the scaling behavior of
components with correlated segments at large scales.
of the mixed signal at
large scales only, since the contribution of the anti-correlated segments at
large scales is negligible. Hence, we next study the scaling behavior of
components with correlated segments at large scales.
For components containing segments with positive correlations
and fixed size ![]() [Fig. 5(c)], we find that at large scales
the slope of
[Fig. 5(c)], we find that at large scales
the slope of ![]() is identical to that expected for a stationary
signal
is identical to that expected for a stationary
signal ![]() (i.e.,
(i.e., ![]() ) with the same correlations [solid line in
Fig. 7(a)]. We also observe a vertical shift in
) with the same correlations [solid line in
Fig. 7(a)]. We also observe a vertical shift in ![]() to lower
values when the fraction
to lower
values when the fraction ![]() of non-zero correlated segments in the
component decreases. We find that after rescaling
of non-zero correlated segments in the
component decreases. We find that after rescaling ![]() by
by ![]() , at large
scales all curves collapse on the curve representing the stationary
correlated signal
, at large
scales all curves collapse on the curve representing the stationary
correlated signal ![]() [Fig. 7(a)]. Since at large scales (
[Fig. 7(a)]. Since at large scales (![]() ), the effect of the zero
segments of size
), the effect of the zero
segments of size ![]() on the r.m.s. fluctuation function
on the r.m.s. fluctuation function ![]() for
components with correlated segments is negligible, even when the zero
segments are 50% of the component [see Fig. 7(a)], the finding of a collapse
at large scales indicates that the vertical shift in
for
components with correlated segments is negligible, even when the zero
segments are 50% of the component [see Fig. 7(a)], the finding of a collapse
at large scales indicates that the vertical shift in ![]() is only due to
the fraction
is only due to
the fraction ![]() of the correlated segments. Thus, to determine the fraction
of the correlated segments. Thus, to determine the fraction
![]() of correlated segments in a nonstationary signal (which is a mixture of
anti-correlated and correlated segments [Fig. 5(a)]), we only need to
estimate at large scales the vertical shift in
of correlated segments in a nonstationary signal (which is a mixture of
anti-correlated and correlated segments [Fig. 5(a)]), we only need to
estimate at large scales the vertical shift in ![]() between the mixed signal
[Fig. 5(d)] and a stationary signal
between the mixed signal
[Fig. 5(d)] and a stationary signal ![]() with identical
correlations.
with identical
correlations.
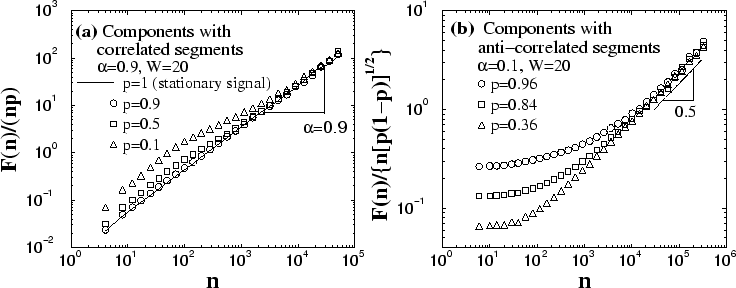 |
For components containing segments with anti-correlations and fixed size ![]() [Fig. 5(b)], we find that at large scales in order to collapse the
[Fig. 5(b)], we find that at large scales in order to collapse the
![]() curves (
curves (![]() ) [Fig. 6(a)] we need to rescale
) [Fig. 6(a)] we need to rescale ![]() by
by ![]() [see Fig. 7(b)]. Note that there is a difference
between the rescaling factors for components with anti-correlated and
correlated segments at small [Figs. 6(a-b)] and large
[Figs. 7(a-b)] scales. We also note that for components with
correlated segments (
[see Fig. 7(b)]. Note that there is a difference
between the rescaling factors for components with anti-correlated and
correlated segments at small [Figs. 6(a-b)] and large
[Figs. 7(a-b)] scales. We also note that for components with
correlated segments (![]() ) and sufficiently small
) and sufficiently small ![]() , there is a
different rescaling factor of
, there is a
different rescaling factor of ![]() in the intermediate scale
regime [see Appendix 7.2, Fig. 10].
in the intermediate scale
regime [see Appendix 7.2, Fig. 10].
For components containing segments of white noise (![]() ), we find no
change in the scaling exponent as a function of the fraction
), we find no
change in the scaling exponent as a function of the fraction ![]() of the
segments, i.e.,
of the
segments, i.e., ![]() for the components at both small and large
scales. However, we observe at all scales a vertical shift in
for the components at both small and large
scales. However, we observe at all scales a vertical shift in ![]() to
lower values with decreasing
to
lower values with decreasing ![]() :
:
![]() .
.