Algoritmo de Máxima Pendiente

    Este método realiza una búsqueda de la solución de Wiener moviéndose por la superficie de error en el sentido negativo del gradiente. Procede de la siguiente manera:

1. Se inicializa el algoritmo con un valor inicial de los pesos del filtro w₀, que ha de dar una idea de la localización del punto óptimo de trabajo. Idealmente, debería ser una estimación de la solución de Wiener, pero si no se posee información previa, se inicializa al vector nulo.
2. Se evalúa el gradiente de la estimación actual.
3. Actualizamos los valores de la estimación del instante actual añadiendo un factor de corrección que apunte al sentido contrario del vector gradiente.
4. Vuelta al paso 2 y repetición del proceso.

    Las correcciones que sucesivamente se aplican a los coeficientes del filtro en la dirección negativa del gradiente conducen al punto de mínimo error cuadrático medio, donde el vector de pesos obtiene su valor óptimo w_opt.

    Denotemos Ñx(n) como el vector gradiente en el instante n. La actualización de los pesos se puede realizar mediante la relación

w(n+1) = w(n) +(1/2) m [-Ñx(n)]

donde m (el tamaño del paso de adaptación) es una constante positiva real. El factor 1/2 es utilizado para simplificar un 2 procedente del gradiente. Y el vector gradiente resulta:

Ñx(n) = -2 p + 2 R w(n)

donde, como sabemos,

x(n) = r_d²(0) - w^H(n)p - p^H w(n) +w^H(n)R w(n)

R = E[x(n) x^H(n)]

p = E[x(n) d*(n)]

    Y la ecuación de actualización de los pesos queda

    Expresión que también puede ser escrita como

ya que  Ñx(n) = -2 E[ x(n) e*(n)].
 

    Debemos observar que si w(n) es la solución de las ecuaciones de Wiener-Hopf, es decir, w(n) es w_opt = R^-1 p, el término de corrección es cero y  w(n+1) = w(n); por tanto, también se anula E[ x(n) e*(n)], y se cumple la condición de ortogonalidad entre datos y error en el punto óptimo de trabajo.
 
 

    Vamos a estudiar ahora la estabilidad del algoritmo.

    Podemos interpretar el método Steepest Descent según el siguiente modelo:

    Puesto que hay una realimentación, existe la posibilidad de que el sistema sea inestable. Según el diagrama, la estabilidad del algoritmo depende de dos factores: el paso de adaptación m y la matriz de correlación R, ya que estos dos parámetros controlan la función de transferencia del lazo de realimentación. Para determinar la condición de estabilidad, vamos a examinar los modos naturales del algoritmo. En particular, utilizaremos la representación de la matriz R en términos de sus autovalores y autovectores para definir una versión transformada del vector de pesos.

    Definimos el vector c(n) que determina el error entre los pesos (diferencia entre el valor actual de los coeficientes y el valor óptimo):

c(n) = w(n) - w_opt

    Sustituyendo, en la ecuación de actualización de los coeficientes,  p por R w_opt  y aplicando la nueva transformación

c(n+1) = (I - mR) c(n)

donde I es la matriz identidad. Esta ecuación representa el modelo siguiente, en el que se enfatiza el hecho de que la estabilidad depende únicamente de m y R.

    Podemos expresar la matriz de autocorrelación en función de la matriz de autovectores, Q y la matriz diagonal de autovalores L como R = Q LQ^H.
    Sustituyendo en la expresión de c(n+1) obtenemos

c(n+1) = (I - mQ LQ^H) c(n)

    Ahora multiplicamos ambos lados por Q^H y aplicamos la propiedad Q^H  = Q ^-1

Q^Hc(n+1) = (I - mL)Q^Hc(n)

    Y definimos un nuevo conjunto de coordenadas

v(n) = Q^Hc(n) = Q^H [w(n) -  w_opt]

de manera que podemos simplificar

v(n+1) = (I - mL)v(n)

    El valor inicial de v(0) es Q^H [w(0) -  w_opt], y suponiendo que al inicio del algoritmo, el vector w(0) se encuentra inicializado al vector nulo, tenemos

 v(0) = - Q^H  w_opt

    El k-ésimo modo natural del algoritmo de máxima pendiente es

v_k(n+1) = (1- m l_k ) v_k(n)    ; k = 1, 2, ..., p

donde l_k es el k-ésimo autovalor de la matriz de correlación R. Esta ecuación representa la versión escalar del modelo anterior, y puede ser visualizada así

    Suponiendo que v_k(n) tiene un valor inicial v_k(0), podemos expresar la anterior ecuación de la forma

v_k(n) = (1- m l_k ) ⁿv_k(0)    ;    k = 1, 2, ..., p

    Según esta serie geométrica, la razón, 1- m l_k, debe ser inferior a 1 para todo valor de k si queremos garantizar la convergencia o estabilidad. Por tanto,

-1 < 1- m l_k< 1

    De esta manera, al crecer el número de iteraciones, n, los modos naturales decrecen en valor y tienden a cero cuando n tiende a infinito. Esto es equivalente a decir que el vector de pesos w(n) tiende a  w_opt cuando n tiende a infinito.

    Puesto que los autovalores de la matriz de autocorrelación R son reales y positivos, la condición necesaria y suficiente para la estabilidad del algoritmo es

donde l_max es el autovalor de máximo valor de la matriz R.
 

    Podemos definir una constante de tiempo t_k, que indique el momento en que el modo k-ésimo decae a 1/e de su valor inicial, así

    La constante de tiempo para dicho modo es

    Si m es lo suficientemente pequeño para considerar que ml_k << 1, la constante de tiempo puede aproximarse por

    Vamos a obtener ahora la evolución del vector de pesos  w(n).

    A partir de la expresión   v(n) = Q^Hc(n) = Q^H [w(n) -  w_opt], si multiplicamos ambos términos por Q, llegamos a

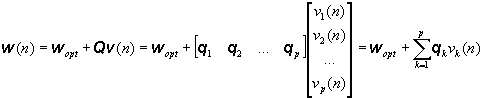
donde los q_i son los autovectores asociados a los autovalores l_i, y v_k(n) es el modo natural k-ésimo definido anteriormente como

 v_k(n) = (1- m l_k ) ⁿv_k(0)

    Si sustituimos esta expresión de v_k(n), obtenemos, para el coeficiente i:

con w_iopt el coeficiente i-ésimo del vector óptimo de pesos y q_ik el elemento i-ésimo del autovector q_k. Esta ecuación nos indica que la convergencia de cada peso depende de todos los autovalores.

    Podemos definir una constante de tiempo global, t, para representar el tiempo que tarda el anterior sumatorio en decaer a 1/e de su valor inicial. Esta constante no puede ser expresada, a priori, de manera sencilla, pero puede acotarse considerando:

• La tasa menor de convergencia se produce cuando q_ik v_k(0) es cero para todo k excepto para el modo correspondiente al menor autovalor l_min. Encontramos, por tanto, un límite superior dado por -1/ln(1-ml_min).
• La tasa mayor de convergencia se produce cuando q_ik v_k(0) es cero para todo k excepto para el modo correspondiente al mayor autovalor l_max. Encontramos, por tanto, un límite inferior dado por -1/ln(1-ml_max).

    De esta manera, tenemos

    Podemos encontrar una expresión más sencilla, si consideramos t como el tiempo que tarda el modo más lento en decaer a 1/e de su valor inicial

    La constante m está acotada por el valor 2 / l_max, así que podemos expresar

con  0 < a <1. Y en términos de a, la constante de tiempo es

donde   c =  l_max / l_min representa la dispersión de autovalores.

    Para finalizar, estudiaremos el comportamiento del error cuadrático medio.

    Partiremos de la expresión del error cuadrático medio:

y sustituimos la expresión de v_k(n)

    Si hemos elegido m de forma que satisfaga la condición de convergencia, el sumatorio tenderá a cero al tender n a infinito,

    Si representamos x respecto al número de iteraciones n, obtenemos una gráfica denomina curva de aprendizaje. Esta curva de aprendizaje consiste en una suma de exponenciales, cada una de las cuales corresponde a un modo natural del algoritmo. En general, el número de modos naturales es igual al número de pesos del filtro. Desde el valor inicial x(0) hasta que decae al valor mínimo x_min, la exponencial decae, para el modo natural k-ésimo, con una constante de tiempo

que para valores pequeños de  m puede aproximarse por

    Observamos el efecto de m en la convergencia  t_k,mse. m debe elegirse de forma que cumpla la condición de estabilidad, pero este valor limita la velocidad de convergencia del algoritmo.
 
 

    Ejemplos

Ir a filtrado adaptativo