Volver al Steepest Descent

    Ejemplo 1.- Steepest - Descent.
 

    Vamos a utilizar el algoritmo Steepest-Descent para encontrar el vector óptimo de un predictor de dos coeficientes . Supongamos que x(n) es ruido blanco de varianza unidad. Por tanto, la matriz de autocorrelación es

y el vector de correlación cruzada

    Con estos valores de R  y p, el vector óptimo está definido por h = 0,  lógico puesto que la predicción igual a cero es la mejor para ruido blanco de media cero.
    El mínimo error cuadrático medio es la potencia de la señal, que es la unidad. Se puede ver a través de la fórmula

x(n) = s_d² - h^H(n) p - p^H h(n) + h^H(n) R h(n)

con s_d² = r_d(0).

    La ecuación de actualización de los pesos queda

h(n+1) = [I- mI] h(n) = (1 -  m) h(n)

    Comenzamos el algoritmo a partir de un valor inicial conocido del vector de pesos

    Los coeficientes deben satisfacer las ecuaciones

h₁(n) =  (1 -  m)ⁿh₁(0)
h₂(n) =  (1 -  m)ⁿh₂(0)

    Los pesos del filtro tienden a su valor óptimo, cero, independientemente del valor inicial, a una velocidad determinada por el parámetro  m. Supongamos unos valores iniciales de

h₁(0) = 1
 h₂(0) = 1/2

y casos distintos, con  m = 0.01 y 0.05. Simulamos una longitud de 400 muestras y representamos el valor de los pesos en cada instante (en rojo, h₁(n), con valor inicial 1, y en azul, h₂(n), con valor inicial 1/2). Observamos que el valor mayor m lleva a la solución óptima más rápidamente.

m = 0.01: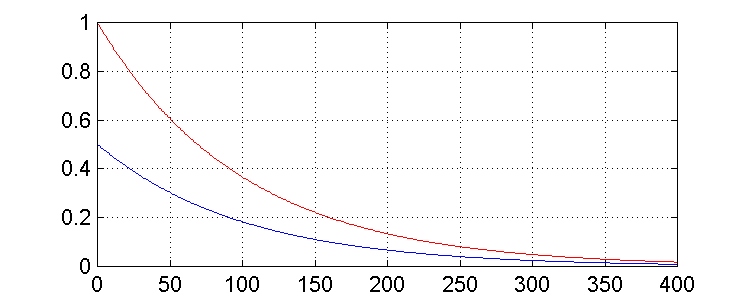

m = 0.05:

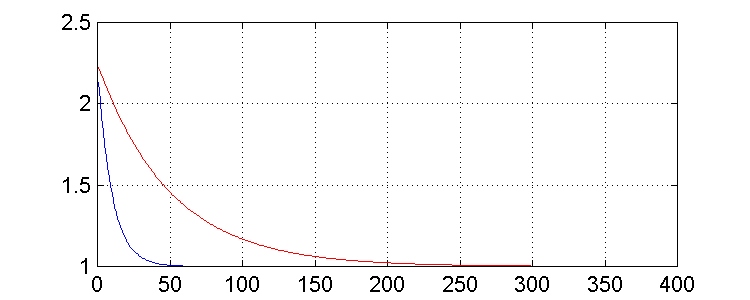
    La expresión del error cuadrático medio es la siguiente:

x(n) = 1 +  (1 -  m)²ⁿh₁²(0) + (1 -  m)²ⁿh₂²(0)

La curva en rojo representa el error cuadrático medio para m = 0.01. Como esperábamos, tiene una caída más lenta hacia el valor nulo que la obtenida con m = 0.05 (curva azul).

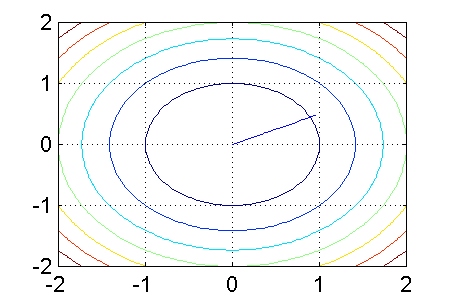
    Podemos obtener una importante visión de la evolución del error si lo representamos frente a los coeficientes h₁(n) y h₂(n). De esta forma, es posible observar los contornos de igual error y la evolución de los coeficientes hacia sus valores óptimos. En la siguiente gráfica, el eje de ordenadas representa valores de  h₂(n) y el eje de abscisas, valores de h₁(n). El punto de partida es h₁(n) = 1  y  h₂(n) = 1/2. Ambos coeficientes evolucionan hasta llegar al óptimo h₁(n) = 0  y  h₂(n) = 0.