PRESTACIONES DEL PERIODOGRAMA

    En esta sección vamos a evaluar las prestaciones del periodograma. Idealmente, al crecer la longitud de los datos, el periodograma debería converger al espectro de potencia del proceso, S_x(e^jw). Pero hemos de ser cautos al tratar la convergencia del periodograma, y puesto que éste es una función de variables aleatorias x(0), ..., x(N-1), es necesario considerar la convergencia en un sentido estadístico. Por ello, vamos a estudiar la convergencia cuadrático-media del periodograma, es decir, evaluaremos si se cumple o no la ecuación

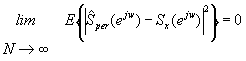
    Para que el periodograma sea un estimador convergente en sentido cuadrático-medio, ha de ser asintóticamente insesgado

y tener una varianza que tienda a cero cuando la longitud de los datos N tiende a infinito,

    Por tanto, el periodogramaha de ser un estimador consistente del espectro de potencia, es decir, ha de converger, en algún sentido, al verdadero valor del espectro estimado.
 

   Comenzamos nuestro estudio con el sesgo o bias. Para ello, calculamos el valor esperado de _x(k), para k=0, 1, ..., N-1

y, para k >= N, el valor esperado es cero. Utilizando la simetría conjugada de _x(k) tenemos

donde w_B(k) es la ventana de Bartlett (triangular)

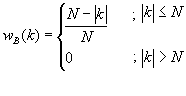
      Hemos obtenido, por tanto, que _x(k) es una estimación sesgada de la autocorrelación. A partir de esta expresión, calculamos el valor medio del periodograma

que es la transformada de Fourier del producto r_x(k)w_B(k). Si aplicamos el teorema de convolución en frecuencia, obtenemos

donde W_B(e^jw) es la transformada de Fourier de la ventana de Bartlett, w_B(k),

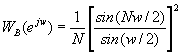
    Por tanto, el valor esperado del periodograma es la convolución del espectro de potencia  S_x(e^jw) con la transformada de Fourier de la ventana de Bartlett, y por consiguiente, el periodograma resulta ser un estimador sesgado. No obstante, como W_B(e^jw) converge a un impulso cuando N tiende a infinito, el periodograma es asintóticamente insesgado.

    El suavizado introducido por la ventana de Bartlett también limita la habilidad del periodograma para discriminar componentes de banda estrecha próximas entre sí. Supongamos, por ejemplo, un proceso aleatorio formado por dos sinusoides en ruido blanco:

x(n) = A₁sin (nw₁ + f₁) +A₂sin (nw₂ + f₂)+ v(n)

donde f₁y  f₂son variables aleatorias incorreladas uniformemente distribuidas y v(n) es ruido blanco con varianza s_v². El espectro de potencia de x(n) es

 S_x(e^jw) = s_v² + (1/2)pdA₁²[d (w-w₁) + d (w+w₁)] + (1/2)pA₂²[d (w-w₂) + d (w+w₂)]

    Y el valor esperado del periodograma es

1/(2p)S_x(e^jw)* W_B(e^jw) = s_v² + (1/4)A₁²[W_B(e^j(w-w1) )+ W_B(e^j(w+w1) )] + (1/4)A₂²[W_B(e^j(w-w2) )+ W_B(e^j(w+w2) )]

    Puesto que la anchura del lóbulo principal de W_B(e^jw ) crece cuando la longitud de los datos decrece, para un valor dado de N, existe un límite en la proximidad de dos sinusoides o procesos de banda estrecha para que dichas componentes puedan ser resueltas o discriminadas. Una forma de definir esta resolución es imponer a Dw la anchura del lóbulo principal del espectro de la ventana W_B(e^jw ), a su "potencia mitad" o a 6 dB. Para la ventana de Barltett, Dw =  0.89 (2p)/N, y esta es, por tanto, la resolución del periodograma.

   Debemos destacar que esta definición de Dw es una regla práctica y debe utilizarse como referencia o guía para determinar la cantidad de datos que es necesaria para una resolución dada. Lo más importante es el hecho de que la resolución es inversamente proporcional a la longitud de datos N. No obstante, aunque esta definición de Dw es algo arbitraria, generalmente se encuentran dificultades para discriminar detalles en el espectro que se encuentran más próximos que esta cantidad.

(ver Ejemplo de Resolución del Peridograma)

    Pasamos ahora a evaluar la varianza del periodograma.

    Sabemos que el periodograma es un estimador asintóticamente insesgado del espectro de potencia, luego, para que sea un estimador consistente, la varianza ha de tender a cero cuando N tiende a infinito. Desafortunadamente, la varianza es un parámetro difícil de calcular, ya que depende de momentos de cuarto orden del proceso. De cualquier modo, vamos a evaluarla para el caso especial de ruido blanco gaussiano.

    Supongamos que x(n) es un proceso blanco gaussiano con varianza s_x². El periodograma puede ser expresado de la siguiente manera:

    Por tanto, el momento de segundo orden del periodograma es

    Vemos que depende de momentos de cuarto orden de x(n). Como x(n) es gaussiano, podemos utilizar el teorema de factorización de momentos y simplicar la expresión anterior. Para variables aleatorias gaussianas complejas, tenemos

    Sustituyendo esta ecuación en la anterior, el momento de segundo orden del periodograma se convierte en una suma de dos términos. El primero contiene productos de E{x(k)x^*(l)}por E{x(m)x^*(n)}. Para ruido blanco, estos productos se igualan a s_x⁴ cuando k = l y m = n, y a cero para otros valores. Por tanto, el primer término se simplifica

    El segundo término, contiene productos de E{x(k)x^*(n)}por E{x(m)x^*(l)}. De nuevo, con ruido blanco, estos términos toman valor distinto de cero para k = n y l = m, siendo s_x⁴ dicho valor. Así, el segundo término queda

    Si aplicamos los resultados obtenidos a la ecuación del momento de segundo orden del periodogram, tenemos

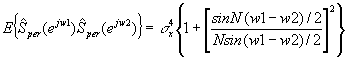
    La expresión de la covarianza es

    Para ruido blanco,

por tanto,

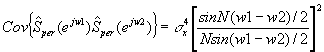
    Finalmente, con w₁ = w₂, obtenemos, para la varianza,

    Observamos que la varianza no tiende a cero cuando N  tiende a infinito, por ello, el periodograma no es un estimador consistente del espectro de potencia. De hecho, como S_x(e^jw) = s_x², la varianza del periodograma de ruido blanco gaussiano es proporcional al cuadrado del espectro de potencia,

(ver Ejemplo Periodograma de Ruido Blanco: estudio de varianza y sesgo)

    Aunque el análisis estadístico para procesos gaussianos no blancos es más difícil, podemos obtener una expresión aproximada para la varianza. Recordamos que un proceso aleatorio x(n) con espectro de potencia S_x(e^jw) puede ser generado filtrando un ruido blanco de varianza unidad v(n) con un filtro lineal tiempo invariante h(n) de respuesta frecuencial H(e^jw), de manera que    |H(e^jw)|² = S_x(e^jw).

    Si x_N(n) y v_N(n) son secuencias de longitud  N  formadas por el enventanamiento de x(n) y v(n), respectivamente, los periodogramas de estos procesos son

    Aunque x_N(n) no es exactamente igual a la convolución de v_N(n) con h(n), si N es grande comparado con la longitud de h(n), los efectos del régimen transitorio se reducen, por tanto,

    Puesto que

la expresión del periodograma de x(n) se puede aproximar como

    Por consiguiente, expresamos la varianza del periodograma

y, dado que la varianza del periodograma de v(n) es la unidad, tenemos

    Así, para valores altos de N, la varianza del periodograma de un proceso aleatorio gaussiano es proporcional al cuadrado de su espectro de potencia.

    El momento de segundo orden y la covarianza pueden generalizarse de forma similar para ruido gaussiano no blanco. Para el momento de segundo orden obtenemos la expresión

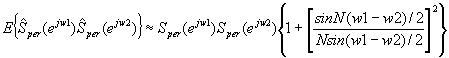
y, para la covarianza,

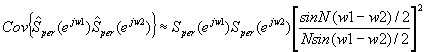
    Para valores altos de N, el término entre corchetes se aproxima a cero si  w₁ - w₂ >> 2p/N, lo que significa que existe poca correlación entre una frecuencia y otra.