SESGO-BIAS Y CONSISTENCIA

    Supongamos que queremos estimar el valor de un parámetro q, a partir de una secuencia de variables aleatorias, x_n, con n = 1, 2, ..., N.
    La estimación obtenida debería ser, en media, igual al valor real. La diferencia entre el valor esperado del estimador y el valor real, q, se denomina sesgo o bias,

    Si el sesgo es cero, entonces el valor esperado del estimador es igual al valor verdadero

y el estimador se denomina insesgado. Si, por el contrario, el sesgo no es cero, se dice que el estimador es sesgado. Si un estimador es sesgado, pero este sesgo tiende a cero cuando el número de observaciones N tiende a infinito,

se dice que es asintóticamente insesgado.

    En general, se desea que el estimador sea insesgado o asintóticamente insesgado.

    Para que el estimador converja a su verdadero valor, es necesario que la varianza del estimador tienda a cero cuando N tienda a infinito,

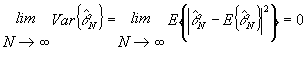
    Si el estimador es insesgado,      y, para un valor e > 0,

    Si la varianza tiende a cero con N tendiendo a infinito, la probabilidad de que el estimador difiera del valor verdadero en una cantidad mayor que e también tenderá a cero. En este caso, se dice que el estimador converge a q con probabilidad uno.

    Además del sesgo y de la consistencia, un estimador también puede definirse por su eficiencia. Decimos que un estimador i es más eficiente que un estimador j si

    Otra forma de convergencia más estricta, es la convergencia cuadrático-media. Se dice que un estimador converge en sentido cuadrático-medio si

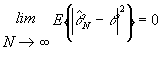
    El estimador es consistente si converge, en algún sentido, al valor verdadero del parámetro. Dependiendo de la forma de convergencia utilizada se pueden dar diferentes definiciones de convergencia. Vamos a considerar que un estimador es consistente si es asintóticamente insesgado y su varianza tiende a cero cuando N tiende a infinito.