Filtro de Wiener IIR no causal

    Para un filtro de Wiener IIR no causal (sin restricciones), debemos determinar la respuesta impulsional, h(n),

que minimice el error cuadrático medio

donde e(n) es la diferencia entre la respuesta deseada d(n) y la salida del filtro de Wiener,

    Para encontrar la respuesta derivamos x respecto a h*(k) para todo k e igualamos las derivadas a cero. Así, obtenemos

o

    Esta ecuación se conoce como principio de ortogonalidad, y establece que x es mínimo y los coeficientes del filtro asumen sus valores óptimos cuando e(n) está incorrelado con cada muestra de entrada x(n) que es utilizada para el cálculo de la estimación. Como consecuencia, el error también es ortogonal a la salida del filtro. Este principio establece una condición suficiente y necesaria para la optimización.

    Ordenando términos llegamos a

    Observamos que el valor medio esperado en la izquierda es la autocorrelación de x(n), y que el término de la derecha es la correlación cruzada entre x(n) y d(n). Por tanto, podemos escribir la ecuación anterior como

    Y así obtenemos las ecuaciones de Wiener-Hopf para el filtro de Wiener IIR no causal.

    Para encontrar una solución a este conjunto de ecuaciones con infinitas incógnitas, expresamos el primer término de las ecuaciones de Wiener-Hopf como la convolución de h(k) con r_x(k),

    En el dominio de la frecuencia,

    Por tanto, la respuesta frecuencial del filtro de Wiener IIR es

y la función de red

    Vamos a evaluar ahora el error cuadrático medio. Partimos de la definición de la función de coste

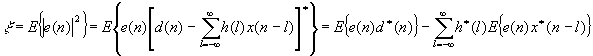
Para el error mínimo, se satisface el principio de ortogonalidad,

y el mínimo error cuadrático medio es

    Utilizando el teorema de Parseval, podemos expresar la ecuación anterior como

    Puesto que

    La expresión de x_min se puede escribir como

    Y en términos de la variable compleja z:

o, equivalentemente,

donde la región de convergencia (ROC) es anular y contiene a la circunferencia unidad.

    Para finalizar, vamos a obtener el filtro óptimo de Wiener en sentido de mínimo error cuadrático medio, para el proceso d(n), si tenemos observaciones ruidosas

para todo n.
    Para hallar H(e^jw), debemos obtener S_x(e^jw) y  S_dx(e^jw). Suponiendo que d(n) y v(n) son procesos incorrelados de media cero, la autocorrelación de x(n) es

y el espectro de potencia

    La correlación cruzada entre d(n) y x(n) es

r_dx(k) = E{d(n)x*(n-k)} = E{d(n)d*(n-k)} + E{d(n)v*(n-k)} = r_d(k)

    Por tanto,

    Y, sustituyendo en la expresión del filtro de Wiener, obtenemos

    Observamos que, para valores frecuenciales en los que S_d(e^jw) es mucho mayor que S_v(e^jw), la relación señal a ruido es alta y |H(e^jw)| es aproximadamente la unidad. Por tanto, en las bandas frecuenciales en las que domina la señal, el filtro deja pasar el proceso con poca atenuación. Por el contrario, para aquellos valores de w en los que la relación señal a ruido es pequeña, es decir, S_d(e^jw) es mucho mayor que S_v(e^jw),  |H(e^jw)| es aproximadamente cero, por lo que en las bandas frecuenciales en las que domina el ruido, el filtro es lo suficientemente pequeño para suprimir el ruido.

    Puesto que S_dx(e^jw) = S_d(e^jw) , si evaluamos el mínimo error cuadrático medio, y aplicamos que S_d(e^jw) es real, tenemos

y sustituyendo la expresión de H(e^jw)

    Y en el dominio z transformado, el mínimo error cuadrático medio es

    Ejemplos

    1.- Filtrado de Wiener IIR no causal
    2.- Filtrado de Wiener IIR no causal. Comparación con filtros FIR e IIR causal.

Ir a filtrado IIR