Filtro de Wiener FIR
![]()
Filtro de Wiener FIR
![]()
Consideremos un filtro causal de longitud p, orden p-1, de respuesta impulsional w(n), y función de red:
![]()
Si x(n) es la entrada al filtro, la salida es la estimación de d(n), obtenida como la convolución de w(n) con x(n)
![]()
Debemos encontrar los coeficientes que minimizan la función de coste
![]()
Por tanto, derivamos x respecto a w*(k) e igualamos las derivadas a cero para los valores posibles de k (k = 0, 1, ..., p-1).
![]()
Con
![]()
la derivada de e*(n) es
![]()
Y sustituyendo obtenemos el principio de ortogonalidad o teorema de proyección:
![]()
Este teorema indica que x es mínimo y los coeficientes del filtro asumen sus valores óptimos cuando e(n) es ortogonal a cada muestra de entrada x(n) que es utilizada para el cálculo de la estimación. Como consecuencia, el error también es ortogonal a la salida del filtro. Este principio establece una condición suficiente y necesaria para la optimización.
Aplicando la expresión del error e(n) tenemos
![]()
Con la suposición de que x(n) y d(n) son procesos estacionarios en sentido amplio (WSS),
E{x(n-l) x*(n-k)} = rx(k-l) y E{d(n) x*(n-k)} = rdx(k),
por tanto,
![]()
Tenemos un conjunto de p ecuaciones lineales con p incógnitas w(k), para k = 0, 1, ..., p-1. En forma matricial, utilizando el hecho de que la secuencia de autocorrelación posee simetría conjugada, rx(k) = rx*(-k), podemos expresar las ecuaciones de Wiener-Hopf como

y en notación vectorial
![]()
donde Rx es la matriz de autocorrelación toeplitz hermítica p x p, w es el vector de coeficientes del filtro, y rdx es el vector de correlación cruzada entre la señal deseada d(n) y la señal recibida x(n).
El error cuadrático medio puede obtenerse de la siguiente manera:

Si los coeficientes w son la solución de las ecuaciones de Wiener-Hopf, E{e(n) x*(n-k)} = 0 y tenemos el error cuadrático medio mínimo
![]()
Tomando el valor esperado,
![]()
Y en notación vectorial
![]()
Como w = Rx-1rdx ,el e.c.m. mínimo puede expresarse en términos de la matriz de autocorrelación Rx y el vector de correlación cruzada rdx:
![]()
De forma más general, este estudio puede realizarse considerando que los coeficientes del filtro pueden ser complejos, y así podemos expresar
|
R wopt = p zmin = rd(0) - pH wopt = rd(0) - woptHR wopt |
donde
![]()
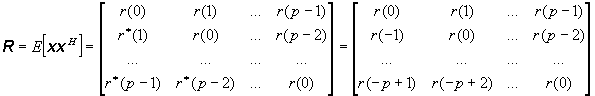
![]()
Existe una interesante interpretación de la superficie de error. Para ello, se expresa el error en su forma canónica, con lo que se pueden observar distintos efectos, como que existe un punto mínimo de error, el significado de los autovalores en la función de error, ...
![]()
![]()