ESTIMACIÓN ESPECTRAL MA

    Un proceso de media móvil puede obtenerse filtrando ruido blanco de varianza unidad, w(n), con un filtro FIR de la siguiente manera:

    La relación entre el espectro de potencia de un proceso MA y los coeficientes b_q(k) es:

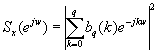
    El espectro de potencia, en términos de la secuencia de autocorrelación r_x(k) puede ser expresado:

donde r_x(k) está relacionado con los coeficientes b_q(k) mediante las ecuaciones de Yule-Walker.

con r_x(-k) = r_x^*(k)  y r_x(k) = 0  para  |k| >q.

    Con un modelo MA, el espectro puede ser estimado de dos formas. La primera de ellas aprovecha el hecho de que la secuencia de autocorrelación de un proceso MA es de longitud finita. Como r_x(k) = 0  para  |k| >q, un estimador utilizado es:

donde suponemos que la estimación de r_x(k) es la apropiada. Notamos que aunque esta estimación es equivalente a la de Blackman-Tukey con una ventana rectangular, existen diferencias en las suposiciones subyacentes en ambos métodos. La ecuación anterior supone que x(n) es un proceso MA de orden q, por lo que la verdadera secuencia de autocorrelación es cero para valores |k| >q. Así, si utilizamos un estimador no sesgado de la secuencia de autocorrelación para |k|<=q:

obtenemos que este estimador es no sesgado. El método de Blackman-Tukey no realiza suposiciones sobre x(n) y podría ser aplicado a cualquier tipo de procesos. Además, debido al enventanado de la secuencia de autocorrelación, a no ser que x(n) sea un proceso de media móvil, el estimador de espectro resultará sesgado.
 

    La segunda técnica de estimación MA consiste en estimar los parámetros b_q(k), a partir de x(n), y posteriormente sustituirlos según la ecuación:

    Ejemplos

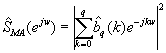
        1.- Estimación de espectro de potencia de proceso MA(4)

    Componente MA