ESTIMACIÓN ESPECTRAL AR



    Un proceso autorregresivo puede obtenerse filtrando ruido blanco de varianza unidad con un filtro todo-polos. El espectro de potencia de un proceso AR de orden p es:

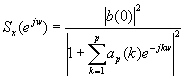
    Si conseguimos estimar los parámetros b(0) y ap(k) a partir de los datos, podremos usar el estimador de espectro:


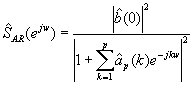
Ecuación de Estimación AR

    La precisión de este estimador depende de la exactitud en la estimación de los parámetros del modelo, así como de si el modelado AR es consistente con la forma en la que los datos son generados. Por ejemplo, si aplicamos este estimador a un proceso MA, es de esperar que los resultados no sean muy precisos.

    Existen diversas técnicas para estimar los parámetros de este modelo. Una vez se han calculado los parámetros necesarios, todos los métodos proceden de igual manera, aplicando la ecuación anterior. En la búsqueda de estos coeficientes, vamos a considerar dos métodos:
 


        Método de Autocorrelación.

    En este método de modelado, los coeficientes ap(k) pueden obtenerse resolviendo las ecuaciones normales de autocorrelación:

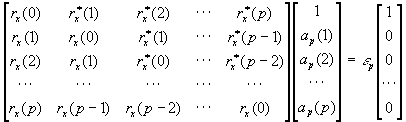
donde

    Calculados los coeficientes ap(k), podemos estimar el parámetro b(0) de la siguiente manera:

    Y con estos parámetros disponibles, ya sólo resta sustituirlos en la "Ecuación de Estimación AR", para obtener la estimación espectral de potencia. En ocasiones, este método se denomina de Yule-Walker, y es equivalente al método de máxima entropía. De hecho, la única diferencia entre los dos métodos reside en la suposición realizada sobre el proceso x(n). Con el método de Yule-Walker se asume que x(n) es un proceso autorregresivo, mientras que en el método de máxima entropía se asume que x(n) es gaussiano.

    Como la matriz de autocorrelación Rx utilizada en las ecuaciones normales es Toeplitz, puede utilizarse la recursión de Levinson-Durbin para resolver las ecuaciones y hallar los coeficientes ap(k). Además, si Rx > 0, las raíces de Ap(z) residirán dentro del círculo unidad. De todas formas, puesto que el método de autocorrelación aplica una ventana rectangular a los datos cuando estima la secuencia de autocorrelación, los datos son extrapolados con ceros. Generalmente, este método produce una resolución menor que otros métodos que no aplican el enventanado a los datos, como ocurre con el método de la covarianza.

    Un fenómeno que puede observarse en este método es la separación espectral, que provoca que un pico en el espectro aparezca como dos picos separados y distintos. Este hecho se manifiesta cuando x(n) es sobreestimado por haber elegido un orden p demasiado alto.

    La estimación de la secuencia de autocorrelación realizada con este método es sesgada, pero podemos modificar este método con una estimación no sesgada:

    En este caso, no se garantiza que la matriz de autocorrelación sea definida positiva, y, como resultado, la varianza de la estimación del espectro tiende a crecer cuando la nueva matriz de autocorrelación está mal condicionada o es singular. Por consiguiente, generalmente se prefiere la estimación sesgada de rx(k).
 
 


        Método de Covarianza.

    Este método calcula los coeficientes ap(k) mediante la resolución del sistema lineal de ecuaciones:

donde

    Estas ecuaciones no son Toeplitz. La ventaja de este método frente al anterior es que no enventana los datos para la estimación de la secuencia de autocorrelación. Para longitudes pequeñas de registros (N), generalmente proporciona una resolución mayor. De todas formas, según crece la longitud de la secuencia de datos y se aleja del orden del modelado, N>>p, el efecto del enventanado se reduce y la diferencia entre ambos métodos llega a ser inapreciable.
 


    Orden de Modelado.

    Un aspecto muy importante a resolver en la estimación espectral AR es la elección del orden p del proceso AR. Si el orden utilizado es demasiado pequeño, el espectro resultante estará suavizado y con poca resolución. Si, por el contrario, es demasiado alto, corremos el riesgo de introducir picos espúreos en el espectro. Por tanto, necesitamos un criterio que indique el orden apropiado para un conjunto concreto de datos. Una forma de elección podría ser incrementar el orden hasta que el error de modelado sea minimizado. Pero existe una gran dificultad en este método, ya que el error decrece de forma monótona a medida que el orden del modelo AR se incrementa. Podemos monitorizar la velocidad de decrecimiento del error y decidir terminar el proceso cuadno ésta se hace relativamente lenta. Sin embargo, esta aproximación puede ser imprecisa y mal condicionada, por lo que resultan necesarios otros métodos.
    Puede obtenerse una solución  incorporando una función de penalización que crezca con el orden p. Se han propuesto diferentes criterios que incluyen un término de penalización que se incrementa linealmente con p:

C(p) = N log ep + f(N) p

    Donde epes el error de modelado, N es la longitud de los datos y f(N) es una constante que debería depender de N. La idea es elegir el valor de p que minimiza C(p). Dentro de esta vertiente distinguimos los siguientes criterios:
 

            Se observa una penalización de 2p por cada coeficiente extra que no reduce significativamente el error de predicción. ep decrece al subir p, por tanto, logep también decrece, pero 2p se incrementa con el incremento de p. En consecuencia, existe un valor mínimo para algún p. Este método proporciona una estimación del orden p demasiado pequeña cuando se aplica a procesos no autorregresivos, y tiende a sobreestimar el orden p según crece N.
            Este criterio incluye el término de penalización (log N) p, que crece con la longitud de los datos y del orden de modelado. Se ha demostrado que MDL es un estimador consistente del orden de modelado, en el sentido de que converge al orden verdadero al crecer el parámetro N.
 
    Akaike también propone otro método de selección de p. Es el criterio del Error Final de Predicción (FPE: Final Prediction Error), que elige el orden p para minimizar el índice de calidad
    Un criterio alternativo ha sido propuesto por Parzen. Se denomina Criterio de la Transferencia Autorregresiva (CAT: Criterion Autoregressive Transfer) y se define
El orden p se selecciona para minimizar CAT(p).
 
      Para secuencias de baja longitud, ninguno de estos métodos funciona particularmente bien. Por consiguiente, estos criterios deberían utilizarse únicamente como "indicadores" del orden de modelado. Debemos considerar también que, como estos criterios dependen del error de predicción ep, el orden p también dependerá de la técnica utilizada para el modelado, es decir, el orden del modelo podría ser diferente para los casos de estimación mediante el método de la autocorrelación y el de la covarianza.
 


    Ejemplos

        1.- Efectos del sobremodelado
        2.- Comparación de métodos: Autocorrelación y Covarianza

    Componente AR