
In this chapter, we have investigated the output of two types of neurophysiologic control systems, one involuntary (heartbeat regulation), and the other voluntary (gait regulation). We find that the time series of both human heart rate and stride interval show ``noisy'' fluctuations. According to classical physiologic paradigms based on homeostasis, such systems should be designed to damp out noise and settle down to a constant equilibrium-like state [41]. However, analysis of both heartbeat and gait fluctuations under apparently steady-state conditions reveals the presence of long-range correlations (see Table 1). This ``hidden'' fractal property is more consistent with a regulatory system driven away from equilibrium, reminiscent of the behavior of dynamical systems near a critical point, or in the case of physiologic systems, perhaps a critical zone of parameter values [40]. The discovery of such long-range organization poses a remarkable challenge to contemporary efforts to understand and eventually simulate physiological control systems. Plausible models must account for such long-range ``memory'' [15, 42]. There are no precedents in classical physiology to explain such complex behavior, which in physical systems has been connected with turbulence and related multi-scale phenomena. The discovery of fractal dynamics as a possibly ``universal'' feature of integrated neural control networks raises the intriguing possibility that the mechanisms regulating such systems interact as part of coupled cascade of feedback loops in a system driven far from equilibrium [43].

The long-range power-law correlations in healthy heart rate and gait dynamics may be adaptive for at least two reasons [21]: (i) the long-range correlations may serve as a newly described organizing principle for highly complex, non-linear processes that generate fluctuations on a wide range of time scales, and (ii) the lack of a characteristic scale may help prevent excessive mode-locking that would restrict the functional responsiveness (plasticity) of the organism. Support for these two related conjectures is provided by the findings described here from severely pathologic states, such as heart failure, where the breakdown of long-range correlations is often accompanied by the emergence of a dominant frequency mode (e.g., the Cheyne-Stokes frequency) (Fig. 1b). Analogous transitions to highly periodic behavior have been observed in a wide range of other disease states, including certain malignancies, sudden cardiac death, epilepsy, fetal distress syndromes, and with certain drug toxicities [5, 6].
Unanswered questions currently under study include: What are the physiological mechanisms underlying such long-range correlations in heartbeat and gait? How do these macroscopic dynamics relate to microscopic fluctuations and self organization at the cellular and molecular levels [44]? Are these fluctuations entirely stochastic or do they represent the interplay of deterministic and stochastic mechanisms [40, 6]?
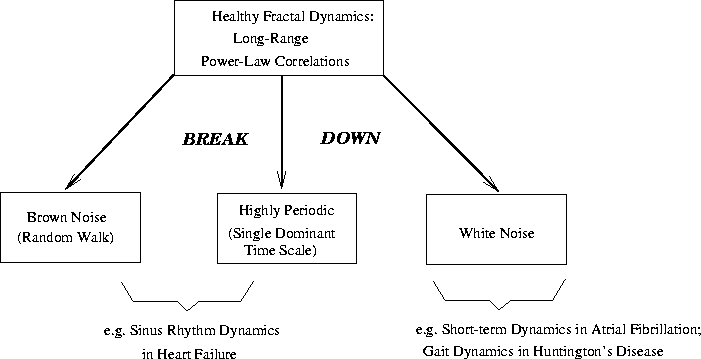
Figure:
The breakdown of long-range power law correlations may lead to any of
three dynamical states: (i) a random walk (``brown noise'') as
observed in low frequency heart rate fluctuations in certain cases of
severe heart failure; (ii) highly periodic oscillations, as also
observed in Cheyne-Stokes pathophysiology in heart failure, as well as
with sleep apnea (Fig. 1c), and (iii) completely
uncorrelated behavior (white noise), perhaps exemplified by the short-term
heart rate dynamics during atrial fibrillation. After
[45].
From a practical viewpoint, these findings may have implications for physiological monitoring. The breakdown of normal long-range correlations in any physiological system could theoretically lead to three possible dynamical states (Fig. 13),[45]: (i) a random walk (brown noise), (ii) highly periodic behavior, or (iii) completely uncorrelated behavior (white noise). Cases (i) and (ii) both indicate only ``trivial'' long-range correlations of the types observed in severe heart failure. Case (iii) may correspond to certain cardiac arrhythmias such as fibrillation, or to gait disorders such as Huntington's disease. Such alterations are not detectable with traditional clinical statistics (e.g., those based upon comparison of means and variances). The application of fractal and related analysis techniques is likely to provide an important, complementary set of tools to assess the stability of such systems and their changes with aging and disease (Figs. 6 and 11). Perhaps most exciting is the prospect that such new approaches may be the basis for the development of dynamical assays designed to assess the efficacy and exclude the toxicity of new interventions, which hopefully will maintain and restore the multi-scale complexity and correlated noisiness that appear to be defining features of healthy, adaptive physiology.