The unexpected observation of fractal variability in human gait raises a number of questions. Does the fractal gait rhythm exist only during walking at one's normal pace, or does it occur at slower and faster walking rates as well?
Does the influence of one stride interval on another continue beyond a few
hundred strides, or do the long-range correlations eventually break
down during an extended walk? To answer these questions, we
asked young healthy men to walk for one hour at
their usual rate as well as at slow and fast paces around an outdoor track [16].
A representative example of the effect of
walking speed on the stride interval fluctuations and long-range
correlations is shown in Fig. 10. Remarkably, the locomotor control
system maintains the stride interval at an almost constant level
throughout the one hour of walking at all three walking speeds. Nevertheless,
both the DFA and power spectral analysis indicate that the subtle variations in walking rhythm are not random. Instead, the time series exhibits long-range correlations at all three walking rates. The fractal scaling indices 
and 
remained fairly constant despite substantial changes in walking
velocity and mean stride interval. For all subjects tested at all three walking rates, the stride interval time series displayed long-range, fractal
correlations over thousands of steps.
These findings indicate that the fractal dynamics of walking rhythm
are normally quite robust and appear to be intrinsic to the locomotor system.
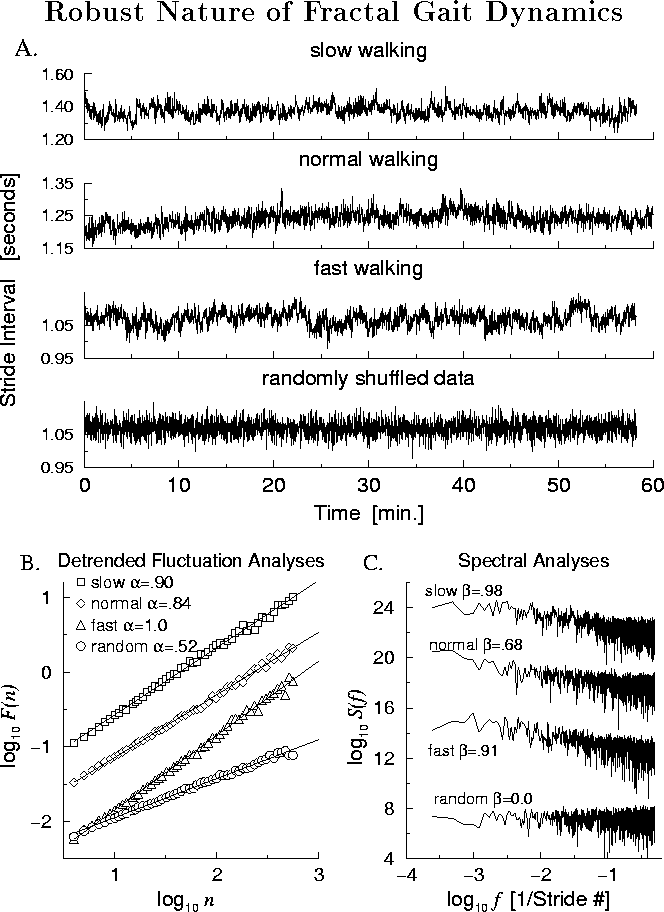
Figure: An example of the effects of walking rate on stride
interval dynamics. A: One hour stride interval time series for
slow (1.0 m/sec), normal (1.3 m/sec), and fast (1.7 m/sec) walking
rates. Note the breakdown of the temporal structure with random re-ordering
of the fast walking trial data points, even though this
shuffled time series has the same mean and standard deviation as the
original, fast time series. B and C: Fluctuation and power spectrum
analyses confirm the presence of long-range correlations at all three
walking speeds and their absence after random shuffling of the data points.
Adapted from [16].