

Next: Signals with different local
Up: Effect of nonstationarities on
Previous: Signals with segments removed
Signals with random spikes
In this section, we consider nonstationarity related to
the presence of random spikes in data and we study the effect of this type
of nonstationarity on the scaling properties of correlated signals. First, we
generate surrogate nonstationary signals by adding random spikes
to a stationary correlated signal 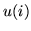 [see Sec. 2 and
Fig. 3(a-c)].
[see Sec. 2 and
Fig. 3(a-c)].
Figure 3:
Effects of random spikes on the scaling behavior of stationary
correlated signals. (a) An example of an anti-correlated signal 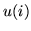 with
scaling exponent
with
scaling exponent 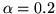 ,
,
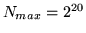 and standard deviation
and standard deviation 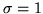 . (b) A series of uncorrelated spikes
(
. (b) A series of uncorrelated spikes
(
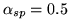 ) at 5
) at 5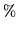 randomly chosen positions (concentration
randomly chosen positions (concentration
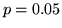 ) and with uniformly distributed amplitudes
) and with uniformly distributed amplitudes 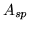 in the
interval
in the
interval ![$[-4, 4]$](img22.png) . (c) The superposition of the signals in
(a) and (b). (d) Scaling behavior of an anti-correlated signal
. (c) The superposition of the signals in
(a) and (b). (d) Scaling behavior of an anti-correlated signal 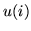 (
(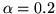 ) with spikes (
) with spikes (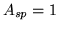 ,
, 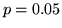 ,
,
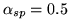 ). For
). For
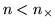 ,
,
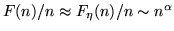 , where
, where
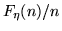 is the scaling function of the signal
is the scaling function of the signal 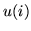 . For
. For 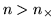 ,
,
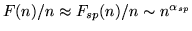 . (e) Scaling behavior of a
correlated signal
. (e) Scaling behavior of a
correlated signal 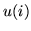 (
(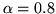 ) with
spikes (
) with
spikes (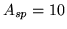 ,
, 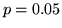 ,
,
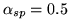 ). For
). For 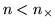 ,
,
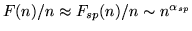 . For
. For 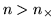 ,
,
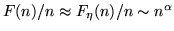 . Note that when
. Note that when
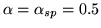 , there is no crossover.
, there is no crossover.
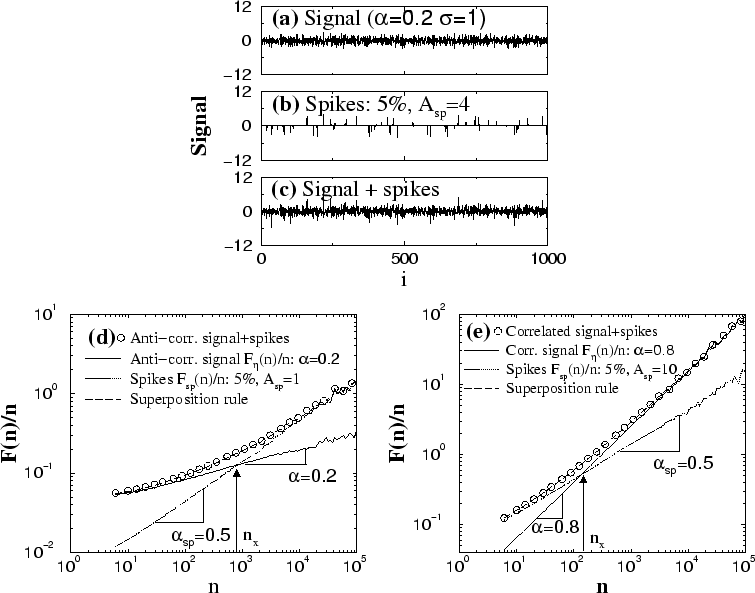 |
We find that the correlation properties of the nonstationary signal with
spikes depend on the scaling exponent 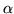 of the stationary signal and
the scaling exponent
of the stationary signal and
the scaling exponent 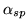 of the spikes.
When uncorrelated spikes (
of the spikes.
When uncorrelated spikes (
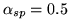 ) are added to a correlated
or anti-correlated stationary signal [Fig 3(d) and (e)], we
observe a change in the scaling behavior with a crossover at a characteristic
scale
) are added to a correlated
or anti-correlated stationary signal [Fig 3(d) and (e)], we
observe a change in the scaling behavior with a crossover at a characteristic
scale 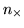 . For anti-correlated signals (
. For anti-correlated signals (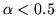 ) with random
spikes, we find that at scales smaller than
) with random
spikes, we find that at scales smaller than 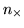 , the scaling
behavior is close to the one observed for the stationary anti-correlated
signal without spikes, while for scales larger than
, the scaling
behavior is close to the one observed for the stationary anti-correlated
signal without spikes, while for scales larger than 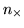 , there is a
crossover to random behavior. In the case of correlated signals
(
, there is a
crossover to random behavior. In the case of correlated signals
(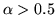 ) with random spikes, we find a different crossover from
uncorrelated behavior at small scales, to correlated behavior at large
scales with an exponent close to the exponent of the original stationary
correlated signal. Moreover, we find that spikes with a very small amplitude
can cause strong crossovers in the case of anti-correlated signals, while
for correlated signals, identical concentrations of spikes with a much larger
amplitude do not affect the scaling.
Based on these findings, we conclude that uncorrelated spikes with a
sufficiently large amplitude can affect the DFA results at large scales for
signals with
) with random spikes, we find a different crossover from
uncorrelated behavior at small scales, to correlated behavior at large
scales with an exponent close to the exponent of the original stationary
correlated signal. Moreover, we find that spikes with a very small amplitude
can cause strong crossovers in the case of anti-correlated signals, while
for correlated signals, identical concentrations of spikes with a much larger
amplitude do not affect the scaling.
Based on these findings, we conclude that uncorrelated spikes with a
sufficiently large amplitude can affect the DFA results at large scales for
signals with 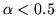 and at small scales for signals with
and at small scales for signals with 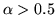 .
.
To better understand the origin of this crossover behavior, we first study the
scaling of the spikes only [see Fig. 3(b)]. By varying
the concentration 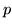 (
(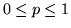 ) and the amplitude
) and the amplitude 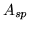 of the
spikes in the signal, we find that for the general case when the spikes may
be correlated, the r.m.s. fluctuation function behaves as
of the
spikes in the signal, we find that for the general case when the spikes may
be correlated, the r.m.s. fluctuation function behaves as
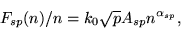 |
(4) |
where 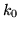 is a constant and
is a constant and 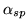 is the scaling exponent of the
spikes.
is the scaling exponent of the
spikes.
Next, we investigate the analytical relation between the DFA results
obtained from the original correlated signal, the spikes and the
superposition of signal and spikes. Since the original signal and the spikes
are not correlated, we can use a superposition rule (see [61]
and Appendix 7.1) to derive the
r.m.s. fluctuation function 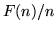 for the correlated signal with spikes:
for the correlated signal with spikes:
![\begin{displaymath}[F(n)/n]^2=[F_{\eta}(n)/n]^2+[F_{sp}(n)/n]^2,
\end{displaymath}](img99.png) |
(5) |
where 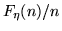 and
and 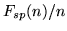 are the r.m.s. fluctuation function for
the signal and the
spikes, respectively. To confirm this theoretical result, we calculate
are the r.m.s. fluctuation function for
the signal and the
spikes, respectively. To confirm this theoretical result, we calculate
![$\sqrt{[F_{\eta}(n)/n]^2+[F_{sp}(n)/n]^2}$](img101.png) [see Figs. 3(d),
(e)] and find this Eq. (5) is remarkably consistent
with our experimental observations.
[see Figs. 3(d),
(e)] and find this Eq. (5) is remarkably consistent
with our experimental observations.
Using the superposition rule, we can also theoretically predict the crossover
scale 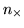 as the intercept between
as the intercept between 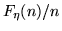 and
and 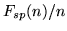 ,
i.e., where
,
i.e., where
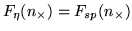 . We find that
. We find that
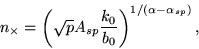 |
(6) |
since the r.m.s. fluctuation function for the signal and the spikes are
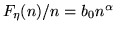 [61] and
[61] and
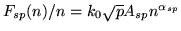 [Eq. (4)],
respectively. This result predicts the position of the crossover depending on
the parameters defining the signal and the spikes.
[Eq. (4)],
respectively. This result predicts the position of the crossover depending on
the parameters defining the signal and the spikes.
Our result derived from the superposition rule can be useful to distinguish
two cases:
(i) the correlated stationary signal and the spikes are independent (e.g., the
case when a correlated signal results from the intrinsic dynamics of the
system while the spikes are due to external perturbations); and (ii) the
correlated stationary signal and the spikes are dependent (e.g., both the
signal and the spikes arise from the intrinsic dynamics of the system). In the
latter case, the identity in the superposition rule is not correct (see
Appendix 7.1).


Next: Signals with different local
Up: Effect of nonstationarities on
Previous: Signals with segments removed
Zhi Chen
2002-08-28
![]() [see Sec. 2 and
Fig. 3(a-c)].
[see Sec. 2 and
Fig. 3(a-c)].

![]() of the stationary signal and
the scaling exponent
of the stationary signal and
the scaling exponent ![]() of the spikes.
When uncorrelated spikes (
of the spikes.
When uncorrelated spikes (
![]() ) are added to a correlated
or anti-correlated stationary signal [Fig 3(d) and (e)], we
observe a change in the scaling behavior with a crossover at a characteristic
scale
) are added to a correlated
or anti-correlated stationary signal [Fig 3(d) and (e)], we
observe a change in the scaling behavior with a crossover at a characteristic
scale ![]() . For anti-correlated signals (
. For anti-correlated signals (![]() ) with random
spikes, we find that at scales smaller than
) with random
spikes, we find that at scales smaller than ![]() , the scaling
behavior is close to the one observed for the stationary anti-correlated
signal without spikes, while for scales larger than
, the scaling
behavior is close to the one observed for the stationary anti-correlated
signal without spikes, while for scales larger than ![]() , there is a
crossover to random behavior. In the case of correlated signals
(
, there is a
crossover to random behavior. In the case of correlated signals
(![]() ) with random spikes, we find a different crossover from
uncorrelated behavior at small scales, to correlated behavior at large
scales with an exponent close to the exponent of the original stationary
correlated signal. Moreover, we find that spikes with a very small amplitude
can cause strong crossovers in the case of anti-correlated signals, while
for correlated signals, identical concentrations of spikes with a much larger
amplitude do not affect the scaling.
Based on these findings, we conclude that uncorrelated spikes with a
sufficiently large amplitude can affect the DFA results at large scales for
signals with
) with random spikes, we find a different crossover from
uncorrelated behavior at small scales, to correlated behavior at large
scales with an exponent close to the exponent of the original stationary
correlated signal. Moreover, we find that spikes with a very small amplitude
can cause strong crossovers in the case of anti-correlated signals, while
for correlated signals, identical concentrations of spikes with a much larger
amplitude do not affect the scaling.
Based on these findings, we conclude that uncorrelated spikes with a
sufficiently large amplitude can affect the DFA results at large scales for
signals with ![]() and at small scales for signals with
and at small scales for signals with ![]() .
.
![]() (
(![]() ) and the amplitude
) and the amplitude ![]() of the
spikes in the signal, we find that for the general case when the spikes may
be correlated, the r.m.s. fluctuation function behaves as
of the
spikes in the signal, we find that for the general case when the spikes may
be correlated, the r.m.s. fluctuation function behaves as