

Next: Strongly correlated segments
Up: Appendix
Previous: Appendix
Superposition rule
Here we show how the DFA results for any two signals 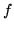 and
and
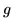 [denoted as
[denoted as 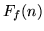 and
and 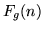 ] relate with the DFA result for the
sum of these two signals
] relate with the DFA result for the
sum of these two signals 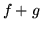 [denoted as
[denoted as 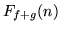 , where
, where 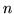 is the box
length (scale of analysis)]. In the general cases, we find
is the box
length (scale of analysis)]. In the general cases, we find
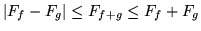 . When the two signals are not
correlated, we find that the following superposition rule is valid:
. When the two signals are not
correlated, we find that the following superposition rule is valid:
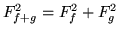 . Here we derive these relations.
. Here we derive these relations.
First we summarize again the procedure of the DFA method[3]. It
includes the following steps: starting with an original signal 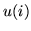 of length
of length
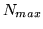 , we integrate and
obtain
, we integrate and
obtain
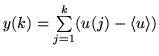 , where
, where
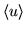 is the mean of
is the mean of 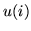 . Next, we divide
. Next, we divide 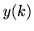 into non-overlapping boxes of equal length
into non-overlapping boxes of equal length 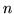 . In each box we
fit the signal
. In each box we
fit the signal 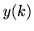 using a polynomial function
using a polynomial function
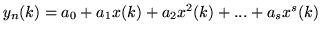 , where
, where 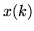 is the
is the 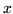 coordinate corresponding to the
coordinate corresponding to the 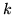 th signal point. We calculate
the r.m.s. fluctuation function
th signal point. We calculate
the r.m.s. fluctuation function
![$F(n)=\sqrt{\frac{1}{N_{max}}\sum\limits^{N_{max}}_{k=1} [y(k)-y_{n}(k)]^2}$](img180.png) .
.
To prove the superposition rule, we first focus on one particular box along
the signal. In order to find the analytic expression of best fit in this box,
we write
![\begin{displaymath}
I(a_0,...,a_s)
=\sum\limits_{k=1}^{n}[y(k)-(a_0+...+a_sx^s(k))]^2,
\end{displaymath}](img181.png) |
(19) |
where
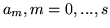 are the same for all points in
this box. ``Best fit'' requires that
are the same for all points in
this box. ``Best fit'' requires that
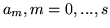 satisfy
satisfy
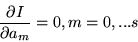 |
(20) |
Combining Eq. (19) with (20) we obtain 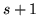 equations
equations
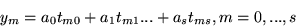 |
(21) |
where
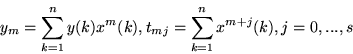 |
(22) |
From Eqs. (21) we determine
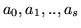 .
.
For the signals 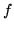 ,
, 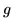 and
and 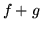 after the integration, in each box we have
after the integration, in each box we have
where 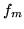 ,
, 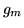 and
and 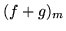 correspond to
correspond to 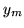 in Eqs. (21).
in Eqs. (21).
Comparing the three groups of equations in Eqs. (23), we find that,
when we add the first two groups together, the left side becomes
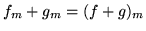 , which is precisely the left side of the third group of
equations. Thus we find
, which is precisely the left side of the third group of
equations. Thus we find
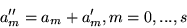 |
(24) |
and for each point 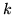 in every box, the polynomial fits for the signals
in every box, the polynomial fits for the signals
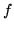 ,
, 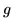 and
and 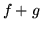 satisfy
satisfy
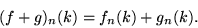 |
(25) |
This result can be extended to all boxes in the signals. For the signal 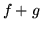 we obtain
we obtain
![\begin{displaymath}
F^2_{f+g}=\frac{1}{N_{max}}\sum\limits_{k=1}^{N_{max}}[f(k)-
f_{n}(k)]^2+[g(k)-g_{n}(k)]^2+2[f(k)-f_{n}(k)][g(k)-g_{n}(k)].
\end{displaymath}](img198.png) |
(26) |
After the substitutions
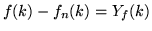 and
and
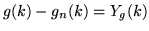 , we rewrite the above equation as
, we rewrite the above equation as
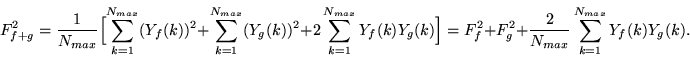 |
(27) |
In the general case, we can utilize the Cauchy inequality
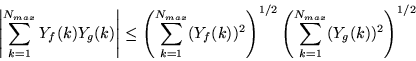 |
(28) |
and we find
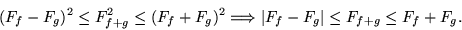 |
(29) |
From Eqs. (21) for 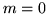 , in every box we have
, in every box we have
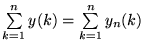 . Thus we obtain
. Thus we obtain
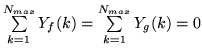 where
where
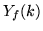 and
and 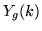 fluctuate around zero.
When
fluctuate around zero.
When 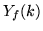 and
and 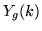 are not correlated, the value of the third
term in Eq. (27) is close to zero and we obtain the following
superposition rule
are not correlated, the value of the third
term in Eq. (27) is close to zero and we obtain the following
superposition rule
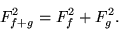 |
(30) |


Next: Strongly correlated segments
Up: Appendix
Previous: Appendix
Zhi Chen
2002-08-28
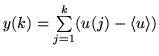 , where
, where
![$F(n)=\sqrt{\frac{1}{N_{max}}\sum\limits^{N_{max}}_{k=1} [y(k)-y_{n}(k)]^2}$](img180.png) .
.
![\begin{displaymath}
I(a_0,...,a_s)
=\sum\limits_{k=1}^{n}[y(k)-(a_0+...+a_sx^s(k))]^2,
\end{displaymath}](img181.png)
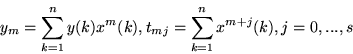
![\begin{displaymath}
F^2_{f+g}=\frac{1}{N_{max}}\sum\limits_{k=1}^{N_{max}}[f(k)-
f_{n}(k)]^2+[g(k)-g_{n}(k)]^2+2[f(k)-f_{n}(k)][g(k)-g_{n}(k)].
\end{displaymath}](img198.png)
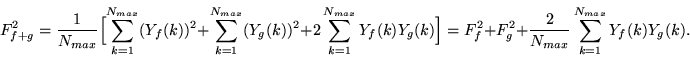
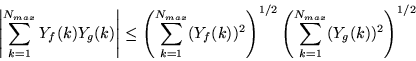
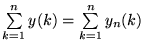 . Thus we obtain
. Thus we obtain
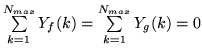 where
where