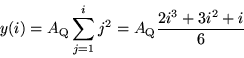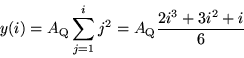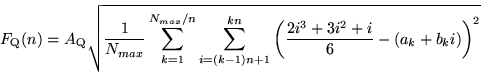Next: Bibliography
Up: Appendix
Previous: DFA-1 on linear trend
DFA-1 on Quadratic trend
Let us suppose now a series of the type
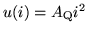 . The integrated time series
. The integrated time series 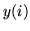 is
is
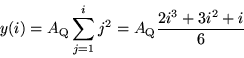 |
(38) |
As before, let us call  and
and  the sizes of the series
and box, respectively. The rms fluctuation function
the sizes of the series
and box, respectively. The rms fluctuation function
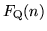 measuring the rms fluctuation is now defined as
measuring the rms fluctuation is now defined as
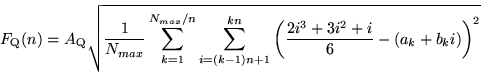 |
(39) |
where 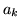 and
and 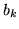 are the parameters of a least-squares fit of
the
are the parameters of a least-squares fit of
the 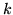 -th box of size
-th box of size  . As before,
. As before, 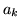 and
and 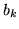 can be determined
analytically, thus giving:
can be determined
analytically, thus giving:
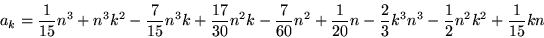 |
(40) |
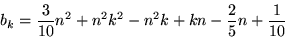 |
(41) |
Once 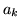 and
and 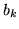 are known,
are known, 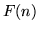 can be evaluated, giving:
can be evaluated, giving:
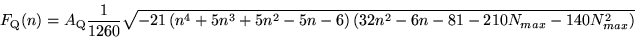 |
(42) |
As 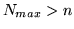 , the dominant term
inside the square root is given by
, the dominant term
inside the square root is given by
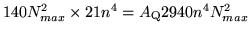 , and then one has approximately
, and then one has approximately
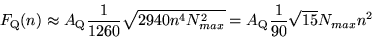 |
(43) |
leading directly to an exponent 2 in the DFA analysis. An interesting
consequence derived from Eq. (43) is that, 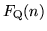 depends on the length of signal
depends on the length of signal  , and the DFA line (
, and the DFA line (
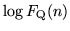 vs
vs 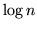 ) for
quadratic series
) for
quadratic series
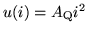 of different
of different  does not overlap (as is the case for linear trends).
does not overlap (as is the case for linear trends).



Next: Bibliography
Up: Appendix
Previous: DFA-1 on linear trend
Zhi Chen
2002-08-28