Volver al Temario

PROBLEMAS DE TRATAMIENTO DIGITAL DE LA SEÑAL

Problemas Tema FILTRADO LINEAL OPTIMO y FILTRADO ADAPTATIVO

1. Dada una observación de una secuencia de la forma x[n]=s[n]+n[n] donde s[n] y n[n] son incorrelados, y donde

encontrar el filtro de Wiener óptimo y el correspondiente error cuadrático medio mínimo para estimar s[n] en el caso de filtro IIR no causal y FIR con longitud P=2 y P=3.
 

2. Una señal aleatoria tiene la siguiente forma x[n]=s [n]+n[n] donde s[n] es una señal aleatoria con densidad espectral compleja

y n[n] es ruido blanco con  e incorrelado con la señal. Encontrar el filtro de Wiener IIR causal para estimar la señal s[n] a partir de x[n], y su error cuadrático medio. Encontrar el filtro IIR no causal y su error cuadrático medio.

3. Cuando la señal de sonar viaja a través del océano está sujeta a dispersión y ruido aditivo. Un modelo simple de la señal recibida es

x[n]=s[n]*b[n]+n[n]

donde b[n] es la respuesta impulsional de un sistema lineal que modeliza el medio océano. Determinar el filtro de Wiener no causal para estimar s[n] donde s es una señal aleatoria con función de correlación

n[n] es ruido blanco con , independiente de la señal, y la respuesta impulsional viene dada por

Determinar también el error cuadrático medio.

4. Encontrar los filtros de error de predicción de primer y segundo orden y la varianza del error de predicción para los procesos aleatorios que tienen como función de correlación:

a) 

b) 

5. Determinar los coeficientes del filtro de error de predicción de orden 1, 2, 3 y 4 y las correspondientes varianzas del error de predicción para un proceso con función de correlación
 

6. Considérese la señal donde x[n]=s[n]+w[n], donde s[n] es un proceso AR(1) que satisface la ecuación en diferencias

s[n]=0.8 s[n-1]+v[n]

donde v[n] es ruido blanco con varianza . Los procesos v[n] y w[n] son incorrelados.

a) Determinar las secuencias de autocorrelación de s[n] y x[n].
b) Determinar el filtro de Wiener IIR no causal para estimar s[n] y su error cuadrático medio.
c) Determinar el filtro de Wiener IIR causal para x[n] y su error cuadrático medio.
d) Determinar el filtro de Wiener FIR de orden 2 para estimar s[n], y su error cuadrático medio.
 

7. Un proceso aleatorio real de primer orden se define por la ecuación en diferencias

x[n]=r x[n-1]+w[m]

donde w[n] es ruido blanco con varianza . La matriz de correlación para orden P es Toeplitz y tiene la forma

 
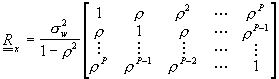
Demostrar que los parámetros del filtro de predicción para este proceso viene dado por

para cualquier orden P>0 y que la varianza del error es igual a  .

8. Un proceso AR(2) se define por la ecuación en diferencias finitas

x[n]=x[n-1]-0.6x[n-2]+w[n]

donde w[n] es ruido blanco con varianza . Utilizar las ecuaciones de Yule-Walker para determinar los valores de .

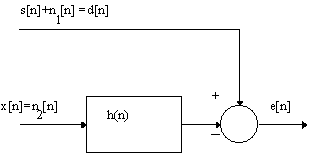
9. Una de las aplicaciones más útiles del procesado adaptativo es la cancelación adaptativa de ruido. Para ello se utiliza una fuente de ruido auxiliar  correlada con el ruido presente en la señal . La señal deseada s[n] y el ruido  son incorrelados.
 

a. Plantear la ecuación del error cuadrático medio y decir cuando se obtiene el error mínimo. Explicarlo haciendo referencia al diagrama de bloques de la figura.



 

En muchas ocasiones se suele aceptar que el ruido  es una versión escalada, retardada y efecto de superposición de  y por tanto se modeliza como combinación lineal =c[n]* .

b. La estructura FIR adaptativa en caso estacionario intenta aproximarse a la solución óptima de Wiener IIR. Demostrar que el filtro óptimo en este caso representa a la función de transferencia que relaciona  y  . ¿Cuánto vale en este caso el error mínimo?

c. Siendo d[n]=cos(w₀n) ; = 1.5w[n-1] + 0.5w[n-2] y =w[n]+0.5w[n-1], calcular el filtro de Wiener FIR de orden 1 y el error mínimo.

d. Determinar la condición de convergencia del parámetro m del algoritmo LMS aplicado a las condiciones del apartado (c).

10. Considerar un proceso autoregresivo (AR) x[n] de orden 1, definido por la ecuación en diferencias

donde v[n] es un ruido blanco de varianza .

1. Utilizar el método de máxima pendiente (Steepest Descent) para el cálculo recursivo de la solución de Wiener para el parámetro a, es decir, definir un filtro predictor adaptativo para el cálculo del parámetro a.

2. Dibujar la curva de error cuadrático medio asociada a este problema, identificando el punto mínimo de la curva en función de los parámetros conocidos.

Determinar la condición de convergencia del parámetro m para asegurar la estabilidad del algoritmo

11. En el diseño de un predictor lineal de la señal x[n], y debido a restricciones de hardware, se ha limitado el número de retardos a 2, de forma que el predictor queda definido como

donde N₁ y N₂ son enteros positivos. El objetivo final es encontrar los valores de a(1), a(2), N₁ y N₂ que minimizan el error cuadrático medio E{e²[n]} donde

Suponiendo que x[n] es un proceso estacionario en sentido amplio y de media cero, se ha estimado la función de autocorrelación de x[n] y se han encontrado los siguientes valores de r_x[k] para k=0,…,7
 

Para k>7 la autocorrelación es aproximadamente cero.

1. Si tuvieras que diseñar un predictor óptimo de la forma , ¿Cuál es el error cuadrático medio cometido en la predicción de x[n]?

2. Repetir el apartado anterior para un predictor de la forma . Comparar con el apartado anterior, dando una explicación del resultado.

3. Derivar una expresión general para el error cuadrático medio mínimo para un predictor de la forma  en función de la autocorrelación de la señal x[n]. ¿Qué valor de N₁ minimiza el error cuadrático medio?

4. Encontrar los valores de a(1), a(2), N₁ y N₂ del predictor de dos coeficientes que minimiza el error cuadrático medio y encontrar el error cuadrático medio cometido por el predictor.

12. Un proceso aleatorio x[n] se define como

donde s[n] es una señal determinista, A es una amplitud aleatoria de media cero y varianza P_o, y v[n] es un ruido blanco incorrelado con varianza . Se toman N muestras del proceso aleatorio y se definen los vectores aleatorios

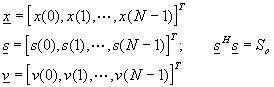
1. Calcular la matriz de covarianzas .

2. ¿Es s un autovector de ?. En caso afirmativo, hallar su autovalor asociado.

3. Sea f_i el i-ésimo autovector de , calcular su autovalor asociado.

4. ¿Cuál es el error cuadrático medio que cometemos si x[n] lo representamos únicamente con el autovector de mayor autovalor?

5. Si , determinar un método que nos permita estimar la potencia de la señal As[n].

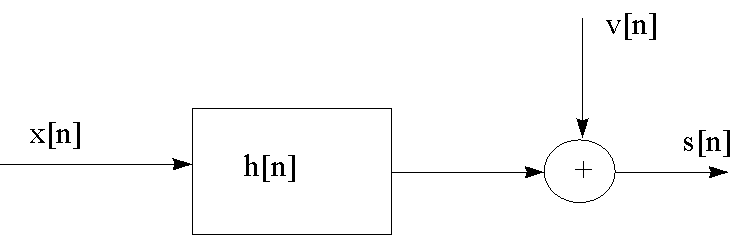
13. En el proceso de identificar un sistema desconocido, vamos a modelarlo como un sistema lineal e invariante al cual se le añade un ruido debido a las imperfeciones del sistema de medida. De este modo la salida del sistema desconocido, a una excitación x[n] conocida, la modelaremos como

donde h[n] es la respuesta impulsional del sistema desconocido y v[n] es un ruido blanco incorrelado con x[n] y de varianza =0.1.

1. ¿Qué propiedades, tanto espectrales como estadísticas, debe cumplir la señal x[n] para simplificar al máximo el proceso de identificación?

2. Si , calcular la secuencia de autocorrelación de s[n] y su densidad espectral de potencia compleja, utilizando como excitación la señal definida en el apartado anterior

 
Para llevar a cabo el proceso de identificación, el método propuesto consiste en diseñar un filtro lineal óptimo al cual se le aplica la misma señal x[n] que al sistema desconocido de forma que su salida, , sea lo mas parecida posible a s[n] en el sentido de mínimo error cuadrático medio.

3. Hacer el diseño del filtro IIR causal óptimo y calcular el error mínimo cometido.

1. Repetir el apartado anterior para el caso de un filtro FIR de orden 1 (2 coeficientes).

En un estudio mas detallado del sistema desconocido, se ha visto que el sistema es lineal pero variante con lo cual los métodos anteriores (apartado c y d) no nos son útiles para identificar el sistema. El nuevo método propuesto utiliza un filtro FIR adaptativo de orden 2. Para implementar el sistema de identificación en un sistema de procesado de señal en tiempo real, se propone utilizar el algoritmo LMS (gradiente instantáneo) sobre la función error definida como

donde k puede tomar cualquier valor entero positivo.

5. Comentar el efecto de k sobre la función error a minimizar.

1. Escribir la ecuación de actualización de los pesos del filtro en el caso de utilizar el algoritmo LMS para minimizar el error J(n).

14. Sea d[n] un proceso AR(1) con función de autocorrelación

con 0 < a < 1. Esta señal ha sido contaminada con un ruido blanco aditivo v[n] incorrelado con d[n] y de varianza . Sea x[n] la señal resultante (x[n]=d[n] + v[n]).

a) Diseñar un filtro de Wiener FIR de primer orden, W(z)=w(0)+w(1)z-1, para reducir el ruido en x[n]. Suponer que a=0.8 y =1.

b) Si se define la relación señal a ruido como

calcular la relación señal a ruido en dB antes y después del filtro de Wiener.

15. Suponer que queremos estimar el espectro de potencia de un proceso AR(2)

x[n]=a(1)x[n-1]+a(2)x[n-2]+w[n]

donde w[n] es un ruido de varianza unidad. Sin embargo, nuestra medida de x[n] es ruidosa, y lo que observamos es el proceso

y[n]=x[n]+v[n]

donde el ruido de medida, v[n], está incorrelado con x[n]. Sabemos que v[n] es un proceso MA(1)

v[n]=b(0)q[n]+b(1)q[n-1]

donde q[n] es un ruido blanco. Basado en la medida de v[n], la densidad espectral de potencia de v[n] estimada es

a) Con esta estimación del espectro de potencia de v[n], dar unos valores para b(0), b(1) y 
 

De la medida de la señal y[n], se han estimado los siguientes valores de la secuencia de autocorrelación ry[k],

2. Estimar la densidad espectral de potencia de x[n] utilizando un modelo paramétrico autoregresivo. ¿Cuanto vale a(1) y a(2) según la estimación realizada?

3. Estimar la densidad espectral de potencia utilizando el método de Blackman-Tukey con ventana rectangular.

4. Si dibujásemos las dos estimaciones del espectro de densidad de potencia, ¿Qué diferencias cabe esperar?.

16. En comunicaciones digitales nos encontramos en muchas ocasiones con que una secuencia de banda ancha se encuentra contaminada por una secuencia de banda estrecha, estando ambas secuencias incorreladas. Normalmente, la señal de banda ancha es la señal deseada, tratándose de una señal de banda ensanchada (Spread-Spectrum) y la de banda estrecha es una interferencia. Nuestro objetivo, desde el punto de vista de filtrado, es diseñar un filtro que suprima la señal de banda estrecha. En la práctica, la banda ocupada por la señal interferente no es conocida, puede ser no estacionaria y la banda de frecuencias que ocupa puede variar con el tiempo.
Suponer que la señal interferente es un proceso armónico definido como

donde w0 es constante, A es una variable aleatoria de media nula y varianza Po=2 y f es una variable aleatoria uniformemente distribuida entre -p y p. La función de autocorrelación de x[n] es

Por otro lado, la señal de banda ancha w[n] tiene la siguiente función de autocorrelación

 
a) Dibujar la densidad espectral de potencia del proceso v[n]=w[n]+x[n]. Suponiendo que la frecuencia w0 es conocida, proponer un tipo de filtro que permita eliminar la señal interferente.

Como la frecuencia interferente w0 es desconocida y puede variar con el tiempo, vamos a diseñar una estructura de filtrado mediante un filtro adaptativo, tal y como se muestra en la figura

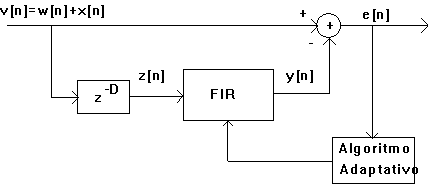
donde el filtro FIR está compuesto por M coeficientes.

2. Calcular las secuencias de correlación 

3. Si D=1 y w0=p/2, diseñar el filtro óptimo de Wiener de orden 1 (M=2). Calcular la potencia de la señal error.

4. Hallar la función de red H(z)=E(z)/V(z). ¿Qué tipo de filtrado realiza?
    

5. ¿Cuál es la función de la unidad de retardo de D muestras?

6. Como resumen, indicar en que parte del circuito recuperamos la señal de banda ancha y en que parte recuperamos la señal de banda estrecha.

7. Escribir la ecuación de actualización de los pesos del filtro si utilizamos el algoritmo LMS. Dar la cota máxima del factor m de actualización de los coeficientes del filtro.

17. Queremos estimar un proceso d(n) a partir de una observación ruidosa del mismo

x(n)= d(n) + v(n)

donde v(n) es un ruido blanco con varianza =1 y d(n) es un ruido estacionario en sentido amplio con una secuencia de autocorrelación cuyos 5 primeros valores son

Suponer que d(n) y v(n) están incorrelados. Nuestro propósito es diseñar un filtro FIR para reducir el ruido en d(n). Por restricciones de hardware, el filtro solo puede tener tres coeficientes distintos de cero.

1. Encontrar el filtro causal óptimo con tres coeficientes

para estimar d(n) y calcular el error cuadrático medio cometido en la estimación.

2. Repetir el apartado anterior para un filtro FIR no causal de la forma

W(z)=w(-1)z^-1+w(0)+w(1)z¹

3. Manteniendo la restricción de un filtro de tres coeficientes, proponer una forma de reducir el error cuadrático medio por debajo de los obtenidos con los dos filtros anteriores. ¿Cuánto vale el error cuadrático medio ?

18. Suponer que queremos estimar una señal d(n) a partir de una observación ruidosa de la misma

x(n)=d(n)+v(n)

donde v(n) es un ruido blanco con varianza unidad que esta incorrelado con d(n). La señal d(n) es un proceso AR(1) que es generado por la ecuación en diferencias

d(n)=0.8d(n-1)+w(n)

donde w(n) es un ruido blanco con varianza =0.36.

1. Calcular el filtro IIR de Wiener causal óptimo para estimar d(n) a partir de x(n). Dar la expresión de H(z) y h(n).

2. Calcular el error cuadrático medio cometido en la estimación.

3. Demostrar que la señal estimada para este problema puede expresarse como

Dar los valores de a y K.

4. La ecuación del apartado anterior representa un filtro estimador recursivo de orden 1. Dibujar el diagrama de bloques de este filtro utilizando el mínimo número de multiplicadores y unidades de retardo.

1. Para un caso general, donde a es conocido y minimiza el error cuadrático medio de la estimación, encontrar el valor de K que también minimiza el error cuadrático medio en la estimación.

Volver al Temario