 Volver
al Temario
Volver
al Temario

PROBLEMAS
DE TRATAMIENTO DIGITAL DE LA SEÑAL
Problemas
Tema CARACTERIZACION DE SECUENCIAS ALEATORIAS
- 1.
-
Para modelar los efectos de redondeo y truncado, las variables
cuantificadas se pueden representar como
![$y[n]=Q{x[n]}=x[n]+e[n]$](img1.gif) ,
donde Q[n] representa el redondeo o el truncado, y
e[n] es el error de cuantificación. Con las
hipótesis adecuadas, es razonable suponer que la secuencia
e[n] es ruido blanco, es decir
,
donde Q[n] representa el redondeo o el truncado, y
e[n] es el error de cuantificación. Con las
hipótesis adecuadas, es razonable suponer que la secuencia
e[n] es ruido blanco, es decir
-
![begin{displaymath}E{(e[n]-m_e)(e[n-k]-m_e)^*)}=sigma_e^2 delta[k] end{displaymath}](img2.gif)
-
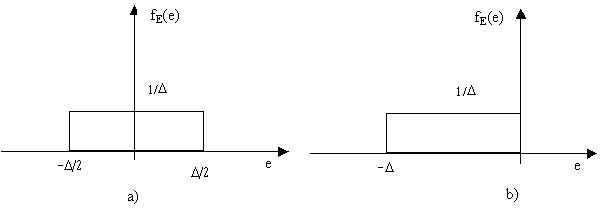
En la figura se muestran las funciones de densidad de probabilidad
del error e[n] de redondeo (a) i de truncado (b).
-
Se pide:
-
a) Determinar la media y la varianza para el ruido debido al
redondeo.
-
b) Determinar la media y la varianza para el ruido debido al
truncado.
- 2.
-
Sea el proceso
-
![begin{displaymath}x[n]=sum_{i=1}^L A_i sin (2pi f_i n + theta_i) + w[n] end{displaymath}](img3.gif)
-
donde las fases iniciales son variables aleatorias independientes
uniformente distribuidas en el intervalo
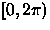 y
w[n] es ruido blanco de varianza
y
w[n] es ruido blanco de varianza 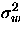 .
Calcular la secuencia de autocorrelación.
.
Calcular la secuencia de autocorrelación.
- 3.
-
Sea x[n] un proceso estocástico discreto real
estacionario de media mx y secuencia de
autocorrelación rx[k]. Sea y[n]
la salida a x[n] de un sistema lineal e invariante de
respuesta impulsional h[n]. Se pide:
-
a) Justificar razonadamente que y[n] es un proceso
estocástico discreto estacionario.
-
b) Determinar la expresión de la media my
del proceso y[n] en términos de mx
y de h[n].
-
c) Determinar las expresiones de las secuencias de autocorrelación
cruzadas de los procesos x[n] e y[n],
es decir, rxy[k], ryx[k]
en términos de rx[k] y h[n].
-
d) Determinar las expresiones de las secuencias de autocorrelación
del procesos y[n], ry[k], en
términos de ryx[k]. Sustituyendo
ryx[k] por la expresión obtenida en
c), expresar ry[k] en términos de
rx[k] y de h[n].
-
e) Aplicando la transformada de Fourier a la expresión
obtenida en el apartado anterior, encontrar la densidad espectral
de potencia del proceso y[n],
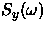 ,
en términos de la densidad espectral de potencia del proceso
x[n],
,
en términos de la densidad espectral de potencia del proceso
x[n], 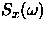 ,
y de la respuesta frecuencial del sistema
,
y de la respuesta frecuencial del sistema 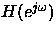 .
.
- 4.
-
Sea x[n] una secuencia de ruido blanco, con media nula
y varianza
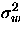 .
Sea x[n] la entrada a la conexión en cascada de
dos sistemas discretos lineales e invariantes en el tiempo como se
muestra en la figura.
.
Sea x[n] la entrada a la conexión en cascada de
dos sistemas discretos lineales e invariantes en el tiempo como se
muestra en la figura.
-
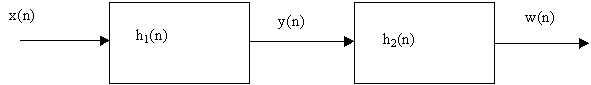
-
a) ¿Es
![$sigma_y^2=sigma_x^2 sum_{k=0}^{infty} h_1^2[k]$](img9.gif) ?
?
-
b) ¿Es
![$sigma_w^2=sigma_y^2 sum_{k=0}^{infty} h_2^2[k]$](img10.gif) ?
?
-
c) Sean
![$h_1[n]=a^n , u[n]$](img11.gif) y
y ![$h_2[n]=b^n , u[n]$](img12.gif) .
Determinar la respuesta impulsional del sistema completo de la
figura, y a partir de ella, determinar
.
Determinar la respuesta impulsional del sistema completo de la
figura, y a partir de ella, determinar 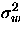
-
d) Si la respuesta dada en el apartado b) ha sido positiva, ¿es
consistente con la respuesta dada en c)?
- 5.
-
Dado que en muchas aplicaciones las secuencias aleatorias discretas
provienen de un muestreo periódico de señales
aleatorias analógicas, en este problema se tratará el
teorema del muestreo de señales aleatorias. Considérese
un proceso estocástico discreto definido por las variables
aleatorias
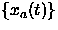 ,
donde t es una variable continua. La función de
autocorrelación se define como
,
donde t es una variable continua. La función de
autocorrelación se define como
-
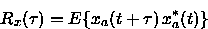
-
y la densidad espectral de potencia es
-
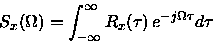
-
Un proceso estocástico discreto obtenido por muestreo
periódico se define por el conjunto de variables
aleatorias
![${x[n]}$](img16.gif) ,
donde x[n]=xa(nT) y T
es el periodo de muestreo.
,
donde x[n]=xa(nT) y T
es el periodo de muestreo.
-
a) ¿Cuál es la relación entre la
autocorrelación del proceso discreto rx[k]
y
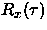 ?
?
-
b) Expresar la densidad espectral de potencia del proceso
discreto
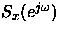 en
términos de
en
términos de 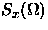 .
.
-
c) ¿Bajo qué condición es
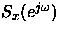 una
representación útil de
una
representación útil de 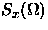 ?
?
- 6.
-
Sea el sistema lineal caracterizado por la ecuación de
recurrencia
-
![begin{displaymath}y[n]=0.8 , y[n-1]+x[n]+x[n-1] end{displaymath}](img20.gif)
-
donde x[n] es un proceso aleatorio estacionario en
sentido amplio de media cero y autocorrelación
![$ r_x[k]=(frac 1 2)^{vert kvert} $](img21.gif)
-
Se pide calcular:
-
a) La densidad espectral de potencia de la salida y[n].
-
b) La autocorrelación ry[k] de la
salida.
-
c) La varianza
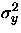 de
la salida.
de
la salida.
- 7.
-
Utilizando la transformada de Fourier, demostrar que la densidad
espectral de potencia de la función de correlación
exponencial
-
![begin{displaymath}r_x[k]= left{ begin{array}{ll} sigma^2 , rho^k](img23.gif)
-
es
-
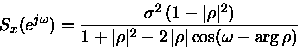
-
Hacer de forma análoga con la transformada z para obtener la
función densidad espectral compleja. Comprobar su
equivalencia particularizando para
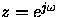
- 8.
-
Determinar las funciones de densidad espectral de potencia
(verificar que son reales y no negativas), las funciones densidad
espectral compleja y su región de convergencia para las
funciones de correlación siguientes:
-
a)
![$ r_x[k] = left{ begin{array}{ll} 3-vert kvert](img26.gif)
-
b)
![$r_x[k] = 2 , (0,6)^{vert kvert} + delta [k] $](img27.gif)
- 9.
-
Determinar la función de autocorrelación
correspondiente a las siguientes funciones de densidad espectral
-
a)
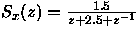
-
b)
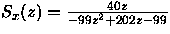
-
c)
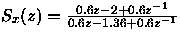
-
d)
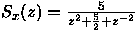
-
e)
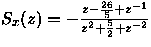
- 10.
-
En este problema se va a demostrar que el módulo al cuadrado
de la función de coherencia satisface
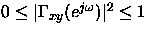 .
.
-
a) Definir un proceso aleatorio
-
![begin{displaymath}v[n]=a_1^*,x[n]+a_2^*,y[n]end{displaymath}](img34.gif)
-
donde a1 y a2 son números
complejos arbitrarios. Demostrar que su función de
correlación viene dada por
-
![begin{displaymath}r_v[k] = left[ begin{array}{ll} a1^*](img35.gif)
-
b) Tomando la transformada de Fourier a esta ecuación y
observando que
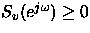 para
cualquier elección de a1 y a2,
demostrar que la matriz de densidad espectral
para
cualquier elección de a1 y a2,
demostrar que la matriz de densidad espectral
-
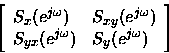
-
es semidefinida positiva.
-
c) Como la matriz de densidad espectral de potencia es semidefinida
positiva, demostrar que esto implica que
-
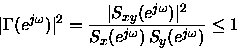
- 11.
-
Las secuencias y[n] y u[n] están
relacionadas por la ecuación en diferencias
-
y[n]=u[n+a]-u[n-a]
-
donde a es una constante. Determinar la función de
correlación de y[n] en términos de la de
u[n].
- 12.
-
Un proceso estocástico real autoregresivo (AR) de orden 1
satisface la relación
-
![begin{displaymath}u[n]+a_1, u[n-1] = w[n]end{displaymath}](img39.gif)
-
donde a1 es una constante, y
![${w[n]}$](img40.gif) es
ruido blanco con
es
ruido blanco con 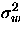 .
Este proceso se conoce como proceso de Markov de primer orden.
.
Este proceso se conoce como proceso de Markov de primer orden.
-
a) Demostrar que si
![${w[n]}$](img40.gif) tiene
media no nula, el proceso AR
tiene
media no nula, el proceso AR ![${u[n]}$](img41.gif) es
no estacionario.
es
no estacionario.
-
b) Para el caso en que
![${w[n]}$](img40.gif) tiene
media nula y la constante a1 satisface la
condición
tiene
media nula y la constante a1 satisface la
condición 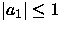 ,
demostrar que la varianza de
,
demostrar que la varianza de ![${u[n]}$](img41.gif) es
es
-
![begin{displaymath}Var{u[n]}=frac {sigma_w^2} {1-a_1^2} end{displaymath}](img43.gif)
-
c) Para las condiciones especificadas en b), encontrar la función
de autocorrelación del proceso AR
![${[u[n]}$](img44.gif) .
Distinguir los casos
.
Distinguir los casos 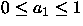 y
y 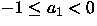 .
.
- 13.
-
Un sistema lineal se define por la ecuación en diferencias
-
y[n]=0.7y[n-1]+x[n]-x[n-1]
-
a) Calcular los primeros 4 valores de ryx[k]
si se conoce
![$r_x=delta[k]$](img47.gif) .
.
-
b) Determinar rxy[k] para -3<k<3.
-
c) Determinar
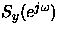
- 14.
-
Un proceso aleatorio x[n] de variables aleatorias independientes con
desidad de probabilidad uniforme
-
![begin{displaymath}f_X[x]= left{ begin{array}{ll} frac{1}{2}](img49.gif)
-
Este proceso se aplica a un sistema lineal invariante con respuesta
impulsional
-
![begin{displaymath}h[n]= left{ begin{array}{ll} frac{1}{2}^n](img50.gif)
-
Sea el proceso de salida y[n]. a) Calcular ryx[k].
b) Calcular ry[k]. c) Calcular Sy(z)
y particularizar para z=ejw.
- 15.
-
Sea el proceso aleatorio
![$x[n]=A cos(pi n/4 + Phi)$](img51.gif) donde
tanto A como
donde
tanto A como 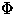 son
variables aleatorias independientes,
son
variables aleatorias independientes, 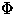 esta
uniformemente distribuida entre 0 y
esta
uniformemente distribuida entre 0 y 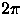 ,
y A es una variable aleatoria de media nula.
,
y A es una variable aleatoria de media nula.
-
a) Calcular la densidad espectral de potencia del proceso.
-
b) Comprobar que se trata de un proceso predecible.
- 16.
-
Factorizar las siguientes densidades espectrales complejas y dibujar
el diagrama de polos y ceros.
-
a)
-
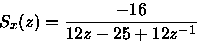
-
b)
-
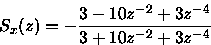
-
c)
-
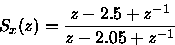
17.
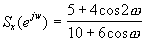
por medio del filtrado de un ruido blanco de varianza unidad con
un filtro lineal e invariante. Encontrar H(z) y h(n) de dicho
filtro.
18.
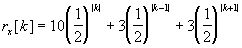
a) Encontrar un filtro que, cuando es excitado por un ruido
blanco de varianza unidad, da como salida un proceso aleatoria con
dicha función de autocorrelación.
b) Encontrar un filtro estable y causal que, cuando es excitado
por el proceso x[n], da como salida un ruido blanco de varianza
unidad.
 Volver
al Temario
Volver
al Temario
![]()

![begin{displaymath}x[n]=sum_{i=1}^L A_i sin (2pi f_i n + theta_i) + w[n] end{displaymath}](img3.gif)
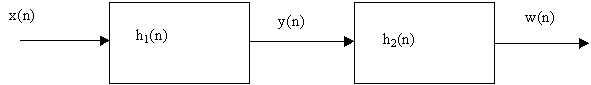
![begin{displaymath}r_x[k]= left{ begin{array}{ll} sigma^2 , rho^k](img23.gif)
![$ r_x[k] = left{ begin{array}{ll} 3-vert kvert](img26.gif)
![begin{displaymath}r_v[k] = left[ begin{array}{ll} a1^*](img35.gif)
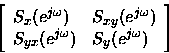
![begin{displaymath}f_X[x]= left{ begin{array}{ll} frac{1}{2}](img49.gif)
![begin{displaymath}h[n]= left{ begin{array}{ll} frac{1}{2}^n](img50.gif)
![]()
![]()