Volver al Temario

PROBLEMAS DE TRATAMIENTO DIGITAL DE LA SEÑAL


 

 Problemas Tema INTRODUCCION

1. Una alternativa para aumentar la resolución frecuencial de la DFT de una secuencia en un margen de frecuencias es la técnica conocida como "zoom FFT", que vamos a estudiar en este problema. Suponer que queremos calcular la DFT en los puntos  y que la secuencia de entrada tiene longitud KL para L entero (la secuencia se puede rellenar con ceros para obtener esta longitud).

  1. Expresando el índice n=l+mL, , demostrar que X[k] podemos calcularla utilizando el siguiente procedimiento :

  1. Estimar el número de multiplicaciones complejas necesarias


 

2. La entrada y salida de un sistema lineal e invariante satisface la ecuación en diferencias

Suponer que disponemos de un programa que implementa la FFT para cualquier secuencia de longitud N=2V. Describir un procedimiento a seguir para calcular con la FFT

donde H(z) es la función de red del sistema.

3. Un banco de filtros está formado por filtros con una respuesta impulsional que cumple

(1)

    1. Calcular la componente polifase P0(z)

    2. Demostrar la siguiente igualdad

    1. ¿Cuánto vale suma la respuesta frecuencial en los puntos w,  w + 2p/M,  ...., w + 2p(M-1)/M ?

    2. Demostrar que la señal original x[n] aplicada a este banco de M filtros se puede recuperar simplemente mediante la suma de las salidas de los filtros de análisis.

    3. Una forma de construir un filtro pasobajo con una respuesta frecuencial que cumpla la condición (1) es mediante el enventanamiento de la respuesta impulsional de un filtro pasobajo ideal con frecuencia de corte en p/M. Calcular la respuesta impulsional de este filtro paso bajo ideal y verificar que se cumple la condición (1).

    4. Otra utilidad de estos filtros es como filtro de interpolación. Demostrar que la señal interpolada tiene exactamente el mismo valor que la señal de entrada al interpolador cada M muestras, siendo M el factor de interpolación. En otras palabras, demostrar que se cumple xi[Mn]=x[n], donde xi[n] es la señal interpolada y x[n] es la señal original.

 

4. Un tipo de banco de filtros muy utilizado en aplicaciones de audio es el banco de filtros en octava. Básicamente, un banco de filtros en octava es un banco de filtros con estructura en árbol con filtros de media banda que se construye aplicando la siguiente regla : En cada nivel, la salida del filtro paso-alto constituye una salida del banco de análisis y la salida del filtro paso-bajo pasa al siguiente nivel donde se aplica la misma división. En el último nivel, tanto la salida del filtro paso-alto como del paso-bajo constituye una salida del bando de análisis.

    1. Diseñar la estructura del banco de filtros de análisis especificando el ancho de banda de la señal de salida de cada filtro para el caso particular de utilizar un banco de análisis con 6 salidas.

    2. Proponer un método de diseño de los filtros y diseñarlos para el caso de utilizar filtros FIR de orden 10.

5. Un multiplexor por división en el tiempo de dos canales, es un dispositivo que acepta dos señales x0[n] y x1[n] y da como salida la señal

    1. Demostrar como se puede realizar este dispositivo con dos interpoladores y elementos de retardo

    2. Demostrar como se puede recuperar las dos señales de y[n] con dos diezmadores y elementos de retardo

6. Un filtro polifase construido para diezmar señales tiene la siguiente estructura

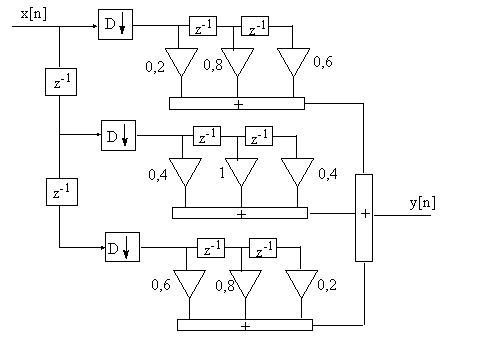
Indicar el factor de diezmado que realiza el filtro y la respuesta impulsional del filtro diezmador.


 
7. Un multiplexor por división en frecuencia de dos canales, es un dispositivo que acepta 2 señales de entrada x0[n], x1[n] y da como salida una señal y[n] de tal forma que y[n] tiene una frecuencia de muestreo doble a las de x0[n] y x1[n], y el espectro de y[n] en la banda de [0,0.25] replica el espectro de x0[n], mientras que el espectro de x1[n] se sitúa entre [0.25,0.5]. Diseñar un dispositivo que permita realizar el proceso de multiplexión por división en frecuencia y otro que permita realizar el proceso inverso de recuperación de las señales x0[n] y x1[n].  

8. El esquema de la figura muestra un transmultiplexor de dos canales.

 

 

 

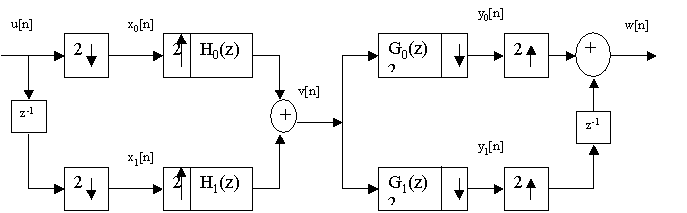
      1. Explicar que trabajo realiza el transmultiplexor

      2. Hallar la relación de la transformada z entre los pares {Y0(z2),Y1(z2)} y el par {X0(z2),X1(z2)}

      3. Si el filtro de síntesis está relacionado con los filtros de análisis

 

 
 Volver al Temario