Vuelta
al Temario
1. Descomposición Polifase
Supongamos una señal x[n] con transformada z
nuestro objetivo va a ser buscar una expresión adecuada para la transformada z cuando cambiamos la razón de muestreo, aumentandola o decrementandola por un facto M. Para ello vamos a factorizar X(z) en elementos separables M muestras.
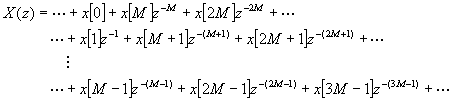
Sacando factor común z-i en cada fila
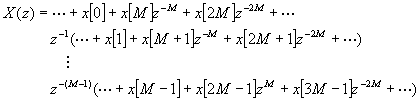
Cada fila la podemos expresar como
El interior del sumatorio no es más que la transformada z de los elementos de x[n] que están separados M muestras.
Se define la componente polifase Pi(z) como
Utilizando esta definición, cada fila de X(z) se puede expresar como
con lo cual
Se define la componente polifase transpuesta
luego la transformada z se puede expresar como
2. Estructuras para Diezmado
En el proceso de diezmado, y para evitar aliasing en la señal diezmada, hay que filtrar previamente la señal a diezmar por un filtro pasobajo con frecuencia de corte p/M, donde M es el factor de diezmado, tal y como se indica en la figura
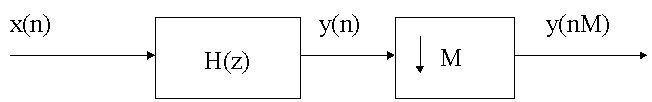
El filtro H(z) suele ser un filtro FIR de fase lineal para no distorsionar la señal x(n) en la banda de paso.
Consideremos los dos sistemas de la siguiente figura
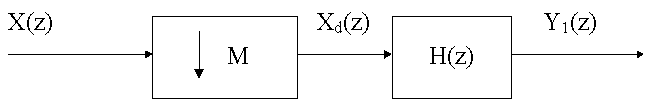
Vamos a demostrar que son equivalentes, con la ventaja que el
primero necesita menos operaciones.
La salida del primer sistema
será:
como 
,
Y2(z)=Y1(z), luego son equivalentes, sin
embargo el primero es mas eficiente computacionalmente