Funciones Matlab utilizadas:

mper.m
welch.m
crossmper.m
crosswelch.m
coherence.m

En este ejemplo vamos a estudiar un procedimiento a seguir para la estimación de la respuesta frecuencial de un sistema desconocido utilizando la estimación de la densidad espectral cruzada entre dos procesos.

Sea x(n) un ruido blanco gaussiano que aplicaremos a un sitema desconocido obteniendo el proceso de salida y(n)=x(n)*h(n)+v(n), donde h(n) es la respuesta impulsional desconocida y v(n) es un ruido aditivo (puede simular ruido de medida).La estimación de la respuesta frecuencial del sistema la realizaremos utilizando la formulación vista en clase

H(w)=Syx(w)/Sx(w)

donde Sxy(w) la estimaremos utilizando el método de welch con la función crosswelch.m y Sx(w) la estimaremos utlizando el método de welch con la función welch.m

La bondad de la estimación la podemos evaluar calculando la coherencia entre la señal y(n) y x(n).
Para ello utilizaremos la función coherence.m. Si la coherencia es próxima a 1 la estimación es muy buena, pero se hay frecuencia en las que la coherencia tiende a 0 entonces es indicativo de que la estimación falla, en este caso por un exceso de ruido de medida.

Para experimentar utilizar el siguiente ejemplo:

x=randn(1024,1);
a=[1, -0.75, 0.5]; % el filtro desconocido es un IIR con este denominador
y0=filter(1,a,x);
K=0.01; % desviacion típica del ruido de medida
y=y0+K*randn(1024,1);
H=crosswelch(y,x,128,0.5,2)./welch(x,128,0.5,2);
% calculamos la funcion de coherencia
Cxy=coherence(c,y,128,0.5,2);
% dibujamos el espectro real
figure(1)
plot(abs(1./fft(a,1024)));
hold on
plot(H,'r');
% dibujamos la función de coherencia
figure(2)
plot(Cxy);
hold on
% variamos el valor de K
K=0.1;
y=y0+K*randn(1024,1);
H=crosswelch(y,x,128,0.5,2)./welch(x,128,0.5,2);
Cxy=coherence(x,y,128,0.5,2);
figure(1)
plot(H,'g');
figure(2)
plot(Cxy,'g');
K=1;
y=y0+K*randn(1024,1);
H=crosswelch(y,x,128,0.5,2)./welch(x,128,0.5,2);
Cxy=coherence(x,y,128,0.5,2);
figure(1)
plot(H,'m');
figure(2)
plot(Cxy,'m');

Respuesta frecuencial exacta del filtro del ejemplo

Estimación de la respuesta frecuencial del ejemplo para diversos niveles de potencia del ruido de medida

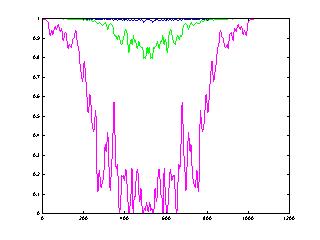
función de coherencia del ejemplo para diversos niveles de potencia del ruido de medida. Podemos ver como el las frecuencias donde la coherencia disminuye el error en la estimación aumenta considerablemente.