Influencia de la ventana en la estimación
![]()
Influencia de la ventana en la estimación
![]()
Sabemos que el periodograma es proporcional al cuadrado de la transformada de Fourier de la señal enventanada: xN(n)=x(n)wR(n),
![]()
A partir de esta expresión, podemos evaluar el valor esperado del periodograma como:
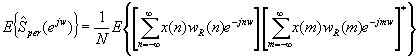
![]()
![]()
Realizamos el cambio de variables k = n-m:
![]()
![]()
donde wB(k) es la ventana de Bartlett:
![]()
Utilizando el teorema de la convolución en frecuencia, el valor esperado del periodograma es:
![]()
con:
![]()
la transformada de Fourier de la ventana rectangular, wR(n).
Observando la ecuación del valor esperado del periodograma deducimos que el suavizado producido en el periodograma viene determinado por la ventana que se aplica a los datos. Aunque la ventana rectangular tiene un lóbulo principal estrecho comparado con otras ventanas, y, por ello, proporciona una cantidad mínima de alisado espectral, tiene lóbulos laterales relativamente grandes, que tienden a enmascarar componentes de banda estrecha de baja potencia. La reducción de amplitud de los lóbulos laterales puede llevarse a cabo a expensas de un incremento en la anchura del lóbulo principal, lo que da lugar a una menor resolución. Esta es la razón por la que el periodograma modificado utiliza distintos tipos de ventanas.
![]()
![]()