Volver al método de Welch 
Ejemplo 1.- Método de Welch.
Supongamos que x(n) es un proceso formado por dos sinusoides en ruido blanco de varianza unidad,
x(n) =A sin(nw1 + f1) + sin(nw2 +f2) + v(n)
con w1 = 0.3 p, w2 = 0.35 p, A =3 y N =512. Consideramos una longitud de sección L = 128, un solape del 50% (por tanto, vamos a tener 2*512/128 - 1 = 7 secciones) y ventana de Hamming.
Visualizamos las estimaciones espectrales de 50 realizaciones diferentes de este proceso, y calculamos el valor medio.
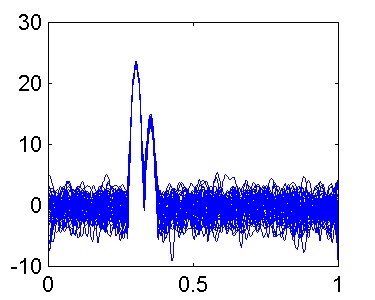
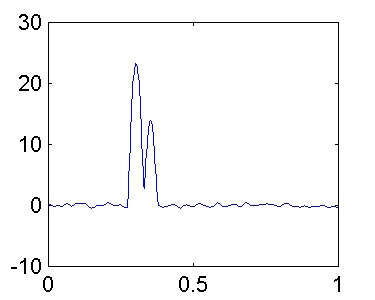
Si comparamos los resultados con los obtenidos aplicando al mismo proceso el método de Bartlett, con N = 512 y K = 8,
observamos:
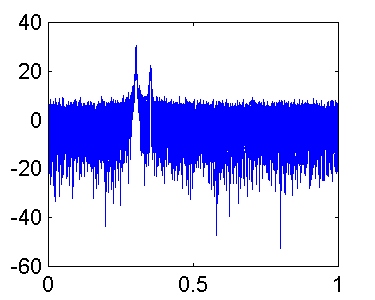
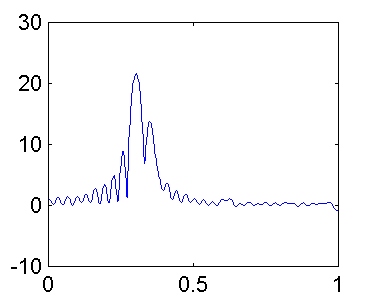
El número de secciones utilizadas en ambos casos es parecido (7 en Welch y 8 en Bartlett). Por tanto, es de esperar que la varianza sea aproximadamente la misma. Notamos que, aunque la anchura del lóbulo principal de la ventana de Hamming aplicada en el método de Welch es 1.46 (1.30 / 0.89) veces más ancha que la ventana rectangular utilizada en el método de Bartlett, la resolución es prácticamente igual. Esto es debido a que el 50% de overlap en el método de Welch permite que la longitud de la sección sea el doble que en el método de Bartlett. En consecuencia, la ganancia obtenida con el método de Welch reside en la reducción de la pérdida espectral a través de los lóbulos laterales de la ventana de datos.