Volver al método de Bartlett 
Ejemplo 1.- Método de Bartlett.
Supongamos que x(n) es un proceso formado por dos sinusoides en ruido blanco de varianza unidad,
x(n) =A sin(nw1 + f1) + sin(nw2 +f2) + v(n)
con w1 = 0.3 p, w2 = 0.35 p, A =3 y N =512. Aplicamos el método de Bartlett con diferentes valores de K para 50 realizaciones y observamos que, al subir K, la varianza disminuye, pero también lo hace la resolución, al disminuir la longitud de las secciones utilizadas en el periodograma, y las sinusoides no son discriminadas con tanta facilidad.
K = 1:
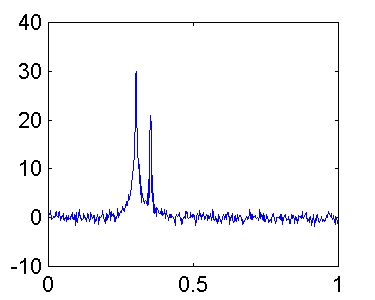
K = 4:
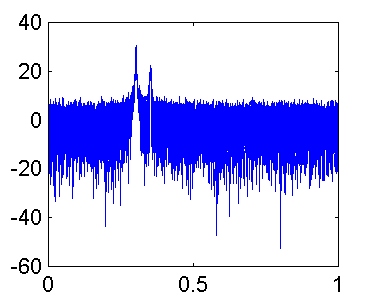
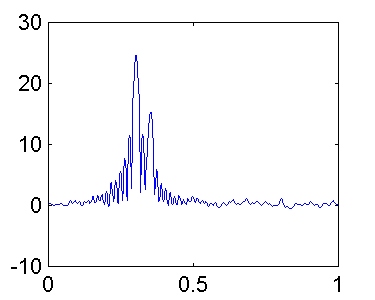
K = 8:
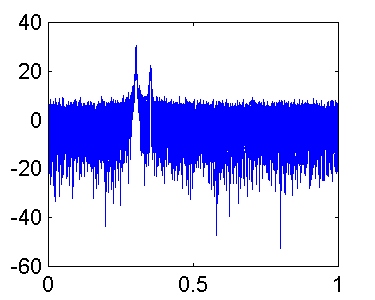
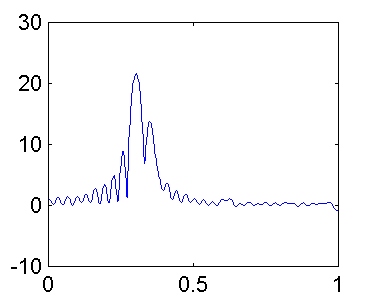
Veamos que ocurre para K = 16:
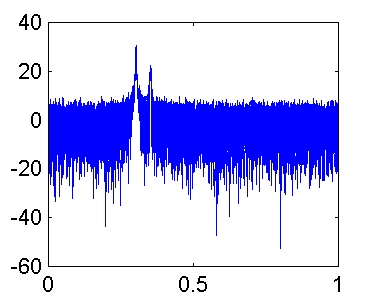
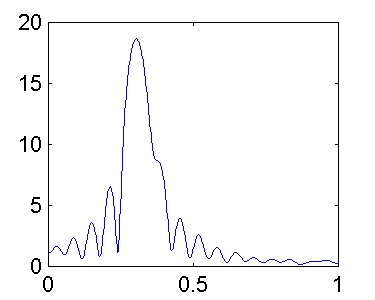
No podemos diferenciar las 2 sinusoides, pues el valor máximo de K que garantiza una resolución aceptable es
K = Dw N /( 0.89 2 p ) = 14
según nos indica la fórmula de la resolución
con
Dw = ( 0.35 p - 0.30 p ) = 0.05 p y N = 512.