Volver al método de Blackman-Tukey

BLACKMAN - TUKEY:

    La expresión general de la varianza del estimador espectral Blackman-Tukey es:

    Comenzamos calculando el valor cuadrático medio.

    A partir de la igualdad

desarrollamos el valor cuadrático

y hallamos el valor medio

    Utilizando la aproximación

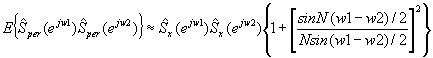
llegamos a una expresión del valor cuadrático medio que consta de dos términos. El primero de ellos es

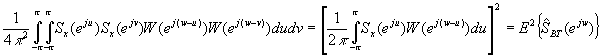
    Este término, al ser introducido en la ecuación inicial, va a ser cancelado por el segundo término de la derecha. Por ello, la varianza es:

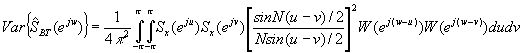
    Puesto que

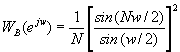
es la transformada de Fourier en tiempo discreto de una ventana de Bartlett, w_B(k),se aproxima a un valor constante al tender N hacia infinito, y W(e^jw) converge a un impulso. Por consiguiente, para valores altos de N, podemos realizar la siguiente aproximación

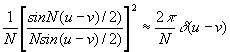
    Es decir, el primer término tiende a un impulso de área 2p/N.

    Por tanto, con N elevado, la varianza del estimador de Blackman-Tukey es, aproximadamente:

    Si M es lo suficientemente grande para considerar que P_x(e^jw) es constante en el lóbulo principal de W(e^j(w-u)), podemos sacar P_x²(e^jw) fuera de la integral:

    Finalmente, aplicando el teorema de Parseval, obtenemos:

con el supuesto N>>M>>1.
 

Volver al método de Blackman-Tukey