

Next: Fractal Dynamics of Human
Up: Fractal Analysis Methods
Previous: Detrended Fluctuation Analysis (DFA)
The self-similarity parameter of an integrated time series is related
to the more familiar auto-correlation function, 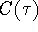 , of the
original (non-integrated) signal. Briefly:
, of the
original (non-integrated) signal. Briefly:
-
For white noise where the value at one instant is completely
uncorrelated with any previous values, the integrated value, y(k),
corresponds to a random walk and therefore
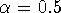 [7, 17]. The auto-correlation function,
[7, 17]. The auto-correlation function, 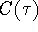 ,
is 0 for any
,
is 0 for any  (time-lag) not equal to 0.
(time-lag) not equal to 0.
-
Many natural phenomena are characterized by short-term correlations
with a characteristic time scale,
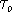 , and an autocorrelation
function,
, and an autocorrelation
function, 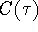 that decays exponentially, [i.e.,
that decays exponentially, [i.e., 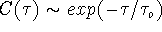 ]. The initial slope of
]. The initial slope of 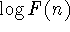 vs.
vs. 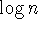 may be different from 0.5, but
may be different from 0.5, but 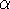 will approach 0.5 for
large window sizes.
will approach 0.5 for
large window sizes.
-
An
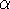 greater than 0.5 and less than or equal to 1.0
indicates persistent long-range power-law correlations, i.e.,
greater than 0.5 and less than or equal to 1.0
indicates persistent long-range power-law correlations, i.e.,
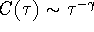 . The relation between
. The relation between 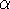 and
and
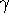 is
is 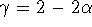 . Note also that the power spectrum,
S(f), of the original (non-integrated) signal is also of a power-law
form, i.e.,
. Note also that the power spectrum,
S(f), of the original (non-integrated) signal is also of a power-law
form, i.e., 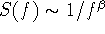 . Because the power spectrum
density is simply the Fourier transform of the autocorrelation
function,
. Because the power spectrum
density is simply the Fourier transform of the autocorrelation
function, 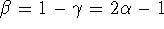 . The case of
. The case of 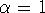 is a
special one which has interested physicists and biologists for many
years--it corresponds to 1/f noise (
is a
special one which has interested physicists and biologists for many
years--it corresponds to 1/f noise (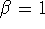 ).
).
-
When
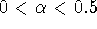 , power-law anti-correlations are present
such that large values are more likely to be followed by small values
and vice versa [10].
, power-law anti-correlations are present
such that large values are more likely to be followed by small values
and vice versa [10].
-
When
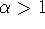 , correlations exist but cease to be
of a power-law form;
, correlations exist but cease to be
of a power-law form; 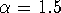 indicates brown noise, the
integration of white noise.
indicates brown noise, the
integration of white noise.
The 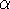 exponent can also be viewed as an indicator of the
``roughness'' of the original time series: the larger the value of
exponent can also be viewed as an indicator of the
``roughness'' of the original time series: the larger the value of
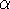 , the smoother the time series. In this context, 1/f noise
can be interpreted as a compromise or ``trade-off'' between the
complete unpredictability of white noise (very rough ``landscape'')
and the much smoother landscape of Brownian noise [18].
, the smoother the time series. In this context, 1/f noise
can be interpreted as a compromise or ``trade-off'' between the
complete unpredictability of white noise (very rough ``landscape'')
and the much smoother landscape of Brownian noise [18].
In the next sections, we apply these scaling analyses to the output of
two complex integrated neural control systems, namely those regulating human
heart rate and gait dynamics in health and disease.


Next: Fractal Dynamics of Human
Up: Fractal Analysis Methods
Previous: Detrended Fluctuation Analysis (DFA)
![]() , of the
original (non-integrated) signal. Briefly:
, of the
original (non-integrated) signal. Briefly:
![]() exponent can also be viewed as an indicator of the
``roughness'' of the original time series: the larger the value of
exponent can also be viewed as an indicator of the
``roughness'' of the original time series: the larger the value of
![]() , the smoother the time series. In this context, 1/f noise
can be interpreted as a compromise or ``trade-off'' between the
complete unpredictability of white noise (very rough ``landscape'')
and the much smoother landscape of Brownian noise [18].
, the smoother the time series. In this context, 1/f noise
can be interpreted as a compromise or ``trade-off'' between the
complete unpredictability of white noise (very rough ``landscape'')
and the much smoother landscape of Brownian noise [18].