 |
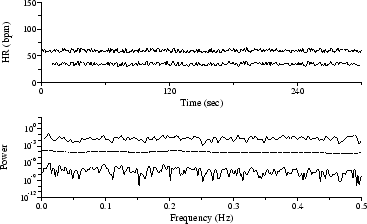
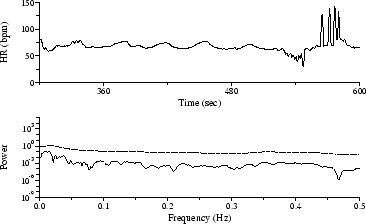
Several HR time series are presented below, together with the corresponding Lomb, FT, and AR spectra. In each case, an irregularly sampled instantaneous heart rate (IHR) signal was obtained from an RR interval time series using the algorithm given in the appendix, and this signal was used as input to the Press-Rybicki algorithm to obtain the Lomb periodogram. A regularly sampled instantaneous heart rate signal[3] was obtained from the same RR series; this signal (five minutes in length in each case, and sampled at 2 Hz) was zero-meaned, detrended, zero-padded to a length of 1024 samples, and Welch windowed, and the result was used as input to standard fast Fourier transform (FT) and autoregressive model (AR) algorithms for PSD estimation[11]. In the examples shown here, the AR models are of order 24. The Lomb and AR spectra can be evaluated for any desired frequencies; for purposes of comparison, all spectra were evaluated at the discrete frequencies defined for the Fourier spectra.
To demonstrate the essential similarity of FT, AR, and Lomb PSD estimates, synthesized HR time series are shown in Figures 1 and 2.
 |
| (1) |
| (2) |
The sequence in Figure 3 was obtained by automated analysis of an ECG signal acquired from a subject with sleep apnea syndrome; the low frequency modulation of heart rate with a period of roughly 45 seconds matches the frequency of the subject's obstructive apneas. Although the spectral peak near 0.025 Hz is most obvious in the AR spectrum, it is also clearly visible in both the Lomb and the FT spectra, which also reveal the harmonically related peak near 0.05 Hz.
The sequence in Figure 4 was obtained by automated analysis of the same signal used in Figure 3, after addition of electrode motion artifact scaled to obtain a signal-to-noise ratio of 12 dB. Roughly 30 QRS detector errors resulting from the added noise are readily discernible in the time series. Although much of the sequence is rejected by the algorithm that prepares input for the Lomb periodogram, the peak near 0.025 Hz is still prominent, and the first harmonic also remains visible. The 0.025 Hz peak is visible but not significant among the clutter in the FT spectrum, and the AR spectrum has no significant features.
By rejecting the outliers and using a predictive interpolator to obtain replacement samples, as shown in Figure 5, the 0.025 Hz peak emerges as a broad feature in the AR spectrum, but the FT spectrum shows a broad, spurious peak at about 0.015 Hz.
Other irregularly-sampled time series frequently appear in HRV-related studies. Among those amenable to Lomb PSD analysis are respiration intervals and tidal volumes, gait, and beat-by-beat systolic blood pressure measurements. As a final example, Figure 6 shows a time series of beat-by-beat measurements of the mean cardiac electrical axis, which fluctuates in response to respiration[12]; the Lomb spectrum clearly reveals the respiratory frequency.
 |