Effect of outliers on the MSE curves

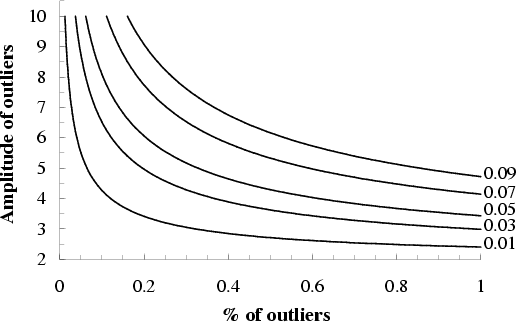
Outliers may affect the entropy values because they change the time series standard deviation and therefore, the value of the parameter r that defines the similarity criterion. Figure 4 shows that a small number of outliers with high amplitude has similar effects on the variance as a higher percentage of outliers with lower amplitude.

Figure 4: Contour plot showing how the percentage of outliers and their amplitude (relative to the mean value of the time series) affects the variance of the time series. Lines connect $(x,y)$ pairs of values that change the variance by the same amount.

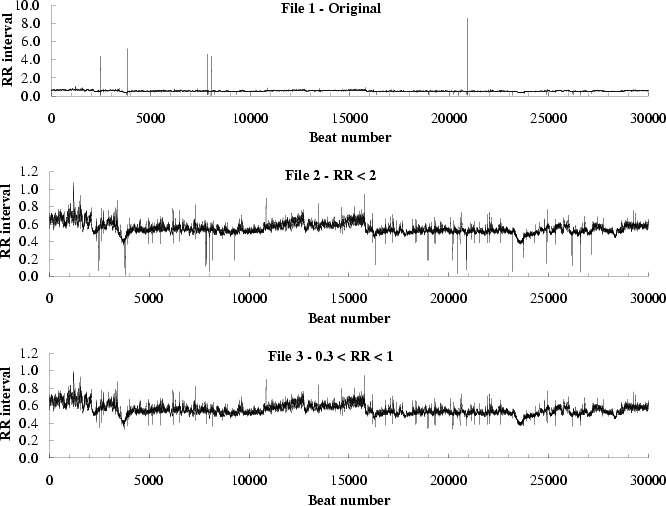
Figure 5 presents three RR interval time series derived from a 24 hour Holter recording of a healthy subject (nsr020). We calculate the MSE curves for a segment of the original time series (file 1) and two filtered time series (file 2 and file 3). File 1 contains the first 30,000 data points (RR intervals) of the original time series. File 2 contains the same data as file 1, but excluding the 6 RR intervals that exceed 2s. Similarly, file 3 contains these same intervals, but excluding the 43 RR intervals that are less than 0.3s or greater than 1s.

Using mse, we can obtain the following MSE analysis of these three files:

    Scale   File 1   File 2   File 3
       1     0.009    0.734    0.734
       3     0.012    0.937    0.933
       5     0.012    1.137    1.140
       7     0.011    1.138    1.144
       9     0.011    1.222    1.210
      11     0.011    1.174    1.224
      13     0.011    1.204    1.186
      15     0.011    1.199    1.186
      17     0.010    1.183    1.189
      19     0.009    1.186    1.212

File 1 includes 6 outliers (225.8, 4.43, 5.24, 4.65, 4.40, 8.61) at least one order of magnitude higher than the mean value of the time series. The sample deviations of the contents of files 1, 2 and 3 are 1.3, 0.62 and 0.60, respectively. For file 1, any two data points $x_i$ and $x_j$ such that $\vert x_i-x_j\vert \leq 0.2$s are not distinguishable. Therefore, this time series seems to be very regular and the entropy values are close to zero. File 3 contains 37 fewer outliers than file 2. However, since the difference between their sample deviations is less than 0.05%, the entropy values are very close. We note that the inclusion of a low percentage of outliers does not significantly affect MSE analysis unless their differences from the mean value of the time series are orders of magnitude larger than the sample deviation.

Figure 5: Top panel: cardiac interbeat (RR) interval time series from a healthy subject (nsr020). One outlier (225.8) is not represented. Middle panel: Time series obtained from the time series presented in the top panel excluding the 6 RR intervals $< 2$s. Bottom panel: Time series obtained from the time series presented in the top panel excluding the 43 RR intervals outside the interval 0.3 to 1s.