
Next: Correlates of physical activity
Up: ECG-based Indices of Physical
Previous: Introduction
Many definitions of heart rate are possible. This study makes use of
both instantaneous heart rate, 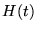 , and mean heart
rate,
, and mean heart
rate,
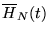 , as defined below.
, as defined below.
Given the sequence of beat arrival times 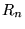 , where
, where 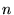 denotes
the beat number, a uniformly sampled instantaneous heart rate signal
may be defined as
denotes
the beat number, a uniformly sampled instantaneous heart rate signal
may be defined as
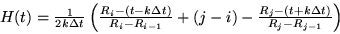 |
(1) |
where 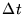 is the desired sampling interval for
is the desired sampling interval for 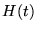 ,
, 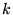 is a
smoothing parameter, and
is a
smoothing parameter, and 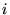 and
and 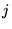 have been chosen such that
have been chosen such that
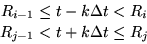 |
(2) |
The middle term (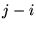 ) in equation (1) thus represents one more than
the number of complete interbeat intervals within a window of width
) in equation (1) thus represents one more than
the number of complete interbeat intervals within a window of width 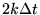 centered on
centered on 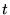 ; the first term is the fraction of the previous
interval within the window, and the last term is the fraction of the final
interval that falls outside the window. From the instantaneous rate
; the first term is the fraction of the previous
interval within the window, and the last term is the fraction of the final
interval that falls outside the window. From the instantaneous rate
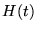 , we derive the mean heart rate:
, we derive the mean heart rate:
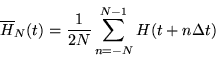 |
(3) |
In the present study,
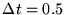 seconds,
seconds, 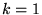 , and
, and 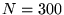 (i.e.,
mean heart rate is determined over a period of
(i.e.,
mean heart rate is determined over a period of
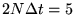 minutes).
minutes).


Next: Correlates of physical activity
Up: ECG-based Indices of Physical
Previous: Introduction
George B. Moody
2002-04-18
![]() , and mean heart
rate,
, and mean heart
rate,
![]() , as defined below.
, as defined below.
![]() , where
, where ![]() denotes
the beat number, a uniformly sampled instantaneous heart rate signal
may be defined as
denotes
the beat number, a uniformly sampled instantaneous heart rate signal
may be defined as